Matematičko modeliranje cena akcija
Apstrakt
Problematika utvrđivanja cena kapitala osnovno je pitanje koje će bit obrađeno u ovom radu. S tim u vezi moramo se osvrnuti i na ulogu hartija od vrednosti, kao finansijskog instrumenta na finansijskom tržištu, odnosno na to da se tržište hartija od vrednosti sastoji iz: emisionog ili primarnog tržišta i sekundarnog tržišta hartija od vrednosti, na kome se vrši promet već izdatih hartija od vrednosti.
Doprinos ovog rada ogleda se u stvaranju komparativne slike finansijske održivosti cena dugoročnih hartija od vrednosti, prvenstveno akcija kao osnovne jedinice akcijskog kapitala koji u svetu predstavlja najveći deo kapitala.
Članak
Uvod
Finansiranje poslovnih subjekata u savremenim tržišnim uslovima zavisi od niza faktora, jedan od njih je i portfolio hartija od vrednosti kojima se formira kapitalna struktura.
Finansijsko tržište je organizovano mesto i prostor u kome se traže i nude finansijsko- novčana sredstva i na kome se zavisno od ponude i tražnje organizovano formira cena tih sredstava.
Ono obuhvata kako organizovane institucije (efektne berze, tržište novca, devizne berze), tako i posredničku trgovinu (tzv. šaltersko tržište) i neposrednu razmenu hartija od vrednosti između izdavalaca i investitora.
Finansijsko tržište predstavlja mehanizam koji dovodi u vezu ponudu i tražnju finansijskih sredstava koja mogu da budu: kratkororočna, kojima se trguje na tržištu novca i dugoročna, kojima se trguje na tržištu kapitala.
Vremenska vrednost novca predstavlja osnovnu dimenziju finansijske održivosti preduzeća, jer uzima u obzir sve faktore koje tržište generiše i s tim u vezi utiče na stvaranje cene kapitala.
Postojanje ova dva segmenta tržišta hartija od vrednosti determiniše i vrste cena hartija od vrednosti koje egzistiraju na finansijskom tržištu. Metodologija utvrđivanja tih cena je upravo ono čime će mo se baviti u ovom radu. Znači, predmet naše analize biće utvrđivanje: nominalne cene ili nominalnog kursa hartija od vrednosti, cene koštanja ili prve kupoprodajne cene ili emisionog kursa hartija od vrednosti i druge i svake dalje kupoprodajne cene, odnosno tržišne cene ili berzanskog kursa hartija od vrednosti.
Definisanje, podela i osnovne karakteristike akcija
Akcije (engl. ѕtock, shares) predstavljaju takve hartije od vrednosti koje odražavaju deo vlasništva nad preduzećem (Poslovni leksikon, Velarta, 2009). One predstavljaju najznačajnije vlasničke hartije od vrednosti i osnovni instrument akcionarskog kapitala.
Vlasništvo nad akcijom kupac stiče ispunjenjem obaveza u novcu, stvarima ili pravima izraženim u novcu.
Jednu od osnovnih karakteristika akcija kao hartija od vrednosti predstavlja veliki broj prava koja donose svojim vlasnicima. Osnovna prava su:
- pravo vlasništva koje se ostvaruje preko prava glasa,
- pravo na učešće u delu dobiti preduzeća (pravo na dividendu),
- pravo preče kupovine akcija,
- pravo na pregled poslovnih knjiga,
- pravo na aktivu u slučaju bankrotstva,
- pravo na transfer akcija.
Akcije mogu biti:
- prema redosledu izdavanja: osnivačke (akcije prve emisije) kada se formira osnivački kapital akcionarskog društva i akcije sledećih emisija koje se emituju radi povećanja kapitala (dokapitalizacije),
- prema pravu glasa: akcije sa pravom glasa i akcije bez prava glasa i
- prema sadržini prava i učešća u dobiti: obične (redovne) akcije i prioritetne (preferencijalne, povlašćene) akcije.
Najpoznatiji tip akcija su obične akcije (Van Horne, Wachowicz, 2005). Njihovom prodajom firma dolazi do sredstava za finansiranje poslovanja a kupci postaju novi suvlasnici firme. Vrednost ovih akcija ako se kotiraju na berzi izražava tržišnu procenu vrednosti preduzeća (Ivaniš, Nešić, 2011). One se nazivaju običnim, jar nemaju posebnih preferencija u pogledu na dividendu ili bankrotstvo. Po svojoj prirodi predstavljaju prava (zahteve) vlasnika preduzeća. Obične akcije daju pravo na učešće u upravljanju, pravo na učešće u dobiti akcionarskog društva i pravo na deo likvidacione mase u skladu sa odlukom o emisiji. Isplata prihoda vlasnicima običnih akcija vrši se posle izmirenja prema vlasnicima obveznica i preferencijalnih akcija, a slično je i u slučaju bankrotstva ili likvidacije firme.
Prava vlasnika običnih akcija na ostatak imovine mlađa su u odnosu na prava vlasnika obveznica i preferencijalnih akcija.
Drugi tip akcija su preferencijalne akcije (Van Horne, Wachowicz, 2005). One predstavljaju neku vrstu hibrida između instrumenata duga i instrumenata akcionarskog kapitala. Kreirane su da bi se povećala sigurnost u pogledu plaćanja u odnosu na običnae akcije. Ova hartija od vrednosti donosi više prihoda vlasnicima nego posedovanje obveznica, ali i veću sigurnost u odnosu na obične akcije. Preferencijalne akcije daju pravo prvenstva na isplatu dividende u odnosu na obične akcije, na isplatu likvidacione mase i na naplatu iz stečajne mase i slučaju stečaja akcionarskog društva.
Dividenda je uglavnom fiksna. Firma nije obavezna da je redovno plaća, ali ne sme plaćati dividendu na obične akcije dok ne isplati dividendu vlasnicima preferencijalnih akcija.
Preferencijalne akcije mogu biti:
- kumulativne, koje daju pravo prvenstva na isplatu svih neisplaćenih dividendi pre isplate dividende po osnovu običnih akcija,
- participativne, koje daju pravo imaocu, pored utvrđene preferencijalne dividende, i na isplatu dividende koja pripada vlasnicima običnih akcija i
- konvertibilne, koje daju pravo imaocu da je može zameniti u običnu akciju.
U daljem radu glavna pažnja biće usmerena na metodologiju utvrđivanja nominalnog, emisionog i berzanskog kursa akcija.
Nominalni, emisioni i berzanski kurs običnih akcija
Analiza cena akcija je od izuzetno velikog značaja, kako za vlasnike akcija, odnosno investitore u njih tako i za sve druge učesnike privrednog i društvenog života. Nivo cena akcija na finansijskom tržištu veoma mnogo govori o kvalitetu poslovanja, efektivnosti i efikasnosti i perspektivama razvoja firmi. Postoji zajednički interes vlasnika, menadžera i zaposlenih da se cene akcija održavaju što je moguće duže na visokom nivou, pošto je to pouzdan signal uspešnosti poslovanja i maksimiranja blagostanja vlasnika.
Postoje tri tipa kursa akcija, i to:
- nominalni kurs,
- emisioni kurs i
- berzanski kurs akcija
Nominalni kurs
Nominalni kurs je iznos na koji akcija glasi. On se odnosi na cenu po kojoj firma vodi emitovane akcije u svom knjigovodstvu. Nominalni kurs određuje se odlukama upravnog odbora firme. Kod određivanja nominalnog kursa mora se voditi računa da to bude zaokružen iznos deljiv sa 10, 100 i 1000 i to bez ostatka.
Pri osnivanju akcionarskog društva emisioni kurs (cena koštanja ili prva kupoprodajna cena) prvo emitovanih (osnivačkih) akcija u principu se poklapa sa njihovim nominalnim kursom.
Kada se akcije prve emisije prodaju po kursu koji je jednak njihovoj nominalnoj vrednosti (nominalnom kursu) formira se akcijski kapital koji je uknjižen na računu kao akcijski kapital po osnovu redovnih (običnih) akcija. Zakonodavstvo zemalja sa razvijenim tržištem hartija od vrednosti kod prve emisije zabranjuje njihov plasman po kursu nižem od nominalnog.
Pored akcija koje imaju nominalnu vrednost postoje i tzv. kvotne akcije koje ne glase na određeni iznos novca. Razlozi za emitovanje ovakvih akcija su: lakše određivanje nove vrednosti akcija u slučaju reorganizacije, lakše emitovanje novih akcija, mogućnost finansiranja akcijama čiji je kurs približno jednak berzanskom i sl. Ove akcije glase na procenat udela vlasnika akcija u ukupnom kapitalu preduzeća, npr.
1/1.000, 1/10.000 (1)
Ako pretpostavimo da je akcionarsko društvo izdalo 200.000 akcija onda imamo da jedna kvotna akcija glasi na 1/200.000 deo akcijskog kapitala tog društva. Prednost ovih akcija je što se kada njihov berzanski kurs postane previsok usled povećanja vrednosti imovine akcionarskog društva, mogu bez ikakvih poteškoća deliti na dve ili više kvotnih akcija. One se kotiraju po komadu, a po komadu se deli i dividenda.
Emisioni kurs
U principu samo se akcije prve emisije plasiraju po kursu koji se poklapa sa njihovom nominalnom vrednošću. Akcije narednih emisija4 plasiraju se po kursu koji je gotovo uvek različit od nominalnog bilo da je on iznad ili ispod njega. Emisioni kurs novih akcija određuje se na bazi berzanskog kursa akcija prethodne emisije. Emisioni kurs nove akcije je zapravo cena po kojoj će prvi kupci kupiti tu novu akciju ali ne za svoje potrebe već za dalju prodaju.
Emisioni kurs nove akcije uključuje i maržu (spred) koja predstavlja naknadu za emisiju i plasman akcija i ona obična iznosi od 1 do 4% od nominalne vrednosti.
Osim marže na visinu emisionog kursa utiče i visina ažija ili disažija odnosno razlika između berzanskog i nominalnog kursa stare ranije emitovane akcije. U slučaju da je berzanski kurs iznad nominalnog imamo ažio, a ako je berzanski kurs isti ili niži od nominalnog imamo disažio (Kočović, 2000).
Ako je npr. nominalni kurs akcije 1.000 din, a berzanski 1.100 din to pokazuje da postoji ažio na akciju nove emisije koji se mora uzeti u obzir u postupku formiranja berzanskog kursa. Ukoliko je nominalni kurs akcije 1.000 din, a berzanski 900 din u postupku formiranja emisionog kursa imali bi disažio.
Sam postupak formiranja emisionog kursa najbolje se može sagledati iz konkretnog primera.
Polazna pretpostavka je da treba formirati emisioni kurs za novoemitovane akcije (evropska praksa) odnosno izvršiti otkrivanje cene za novoemitovane akcije (američka praksa). Stare, ranije emitovane akcije, istog emitenta po nominali od 1.000 din za godinu dana dostigle su kurs od 1.100 din i isplaćenu dividendu od 180 din po akciji. Postavlja se pitanje po kom kursu će biti plasirane novoemitovane akcije na primarnom tržištu kapitala ako je standardna marža nove emisije npr. 2% odnosno 20 din.
Na osnovu datih pretpostavki odgovor koliki će biti emisioni kurs nove akcije će biti:
E.K. nove akcije = B.K. stare akcije + spred + godišnja kapitalizacija (isplaćena dividenda) odnosno,
E.K. nove akcije = 1.100 + 20 + 180 = 1.300 din. (2)
Znači, emisioni kurs nove akcije iznosio bi 1.300 din. To bi bio tzv. test kurs ili početni emisioni kurs za nove akcije (evropska praksa) ili prvootkrivena cena (američka praksa).
Emisija novih akcija je specifičan oblik emisionog posla kako za emitenta tako i za svakog berzanskog posrednika odnosno agenta. Ova specifičnost izražena je pre svega u karakteristikama koje u sebi sadrže nove akcije i u tehnologijama rada koje se primenjuju na primarnom tržištu akcija u skladu sa tim karakteristikama.
Nove akcije su vrsta akcija koje služe za povećanje akcionarskog kapitala, a sama emisija novih akcija može biti:
- zatvorenog karaktera u kojoj akcije mogu kupovati samo postojeći akcionari - emisija za poznatog kupca i
- otvorenog karaktera (javna emisija za nepoznatog kupca) u kojoj se akcije plasiraju na primarnom tržištu kapitala na isti način na koji se vrši plasman i svih drugih efekata ali pod drugačijim uslovima.
Za nove akcije vezano je i pravo preče kupovine. Pravo preče kupovine je pravo pravo akcionara da kupe novu akciju pre svakog drugog novog akcionara. To pravo se definiše donošenjem odluke o emisiji novih akcija.
Kada je emisioni kurs nove akcije koja se nudi akcionaru koji ima pravo preče kupovine jednak nominalnom, odnosno berzanskom kursu tada je reč o ''al pari'' kursu prava preče kupovine.
Pravo preče kupovine omogućuje starim akcionarima da koristeći to svoje pravo ostvare jedan broj besplatnih akcija. Na taj način stari akcionari za ukupan broj kupljenih novih akcija mogu ostvariti kupovnu cenu nižu od emisionog kursa što predstavlja naplatu riziko premije za njihov ranije investiran akcionarski kapital. Za nove akcionare ta razlika u nabavnoj vrednosti novih akcija je u stvari samo cena ulaznice u akcionarsko društvo koje se uspešno razvija. Dakle, stari akcionari u odnosu na nove imaju pravo da kupe nove akcije ne samo po istom nego i po nižem emisionom kursu.
Pravo preče kupovine, osim ''al pari'' kursa, može imati i tzv. diskontni kurs. To je slučaj kada se emisija prava preče kupovine ostvaruje po kursu koji je ispod nominalnog kursa nove akcije. To je u stvari emisija prava preče kupovine uz diskont.
Osnovni smisao emisije novih akcija sa pravom preče kupovine uz diskont je mogućnost davanja šanse postojećim akcionarima da zarade na prodaji prava preče kupovine (Kočović, 2000). Pri emisiji novih akcija sa diskontom najčešće je samo određeni broj njih namenjen starim akcionarima sa pravom preče kupovine.
Emisijom novih akcija sa pravom preče kupovine uz diskont omogućeno je starom akcionaru da kupi jeftino, ili da jeftino kupi samo jedan deo a drugi deo prava da proda, ili pak da koristi svoju treću mogućnost i da svoje pravo u celosti proda drugome. Iznos diskonta se obično kreće od 1 do 20% od tekućeg berzanskog kursa akcija. Ako se pravo ne iskoristi, smanjiće se proporcija učešća akcionara u strukturi kapitala i nastaće gubitak zbog smanjenja cene akcija u periodu kada se one prodaju bez prava (Krasulja, Ivanišević, 2007).
Vrednost prava preče kupovine moguće je izraziti pomoću sledeće formule:

Na ovaj način stari akcionar svaku akciju dobija jeftinije za 171,67 dinara što praktično znači da će za lot kupljenih akcija od 100 komada platiti umesto 60.000 din (600 din ´ 100 kom.=60.000 din), samo 42.833 din [100 kom. ´ (600 - 171,67)=42.833 din]. Odnosno za 60.000 din kapitala akcionar će umesto 100 kom. akcija koristeći pravo preče kupovine doći u posed vlasništva od 140 kom. akcija (60.000 : 428,33=140,07).
U momentu puštanja u promet akcija sa pravom preče kupovine stare akcije se u principu kotiraju sa umanjenim kursom u visini prava preče kupovine, odnosno stare akcije se prodaju po svom kursu umanjenom za vrednost prava, što u datom primeru znači po kursu od 828,33 din za akciju (1.000 - 171,67 = 828,33 din). Ukoliko bi sve nove emitovane akcije bile zatvorenog tipa i bez prava preče kupovine onda bi takve emisije akcija onemogućile poslovno i upravljačko restrukturiranje akcionarskih društava, odnosno njihovo oslobađanje od loših partnera i loših poslova čime se sprečava dolazak novih akcionara i novih menadžera sa novim idejama (Kočović, 2000).
Berzanski kurs
Berzanski kurs ili tržišna cena akcija je ustvari novčani iznos po kome se ostvaruje druga i svaka dalja kupoprodaja akcija na sekundarnom finansijskom tržištu (u okviru berzanskog ili vanberzanskog prometa) kroz odnose ponude i tražnje. Berzanski kurs je kurs po kome se obavljaju kupoprodajne transakcije između kupaca i prodavaca.
Berzanski kurs se utvrđuje svakoga dana od dana prve prodaje akcija na sekundarnom tržištu. Ovo svakodnevno formiranje kursa naziva se kotacija. Znači, sve što se dešava sa berzanskim kursom akcija na finansijskom tržištu od momenta emisije (završetka plasmana) do kraja životnog veka preduzeća podrazumeva njegovo kretanje na sekundarnom tržištu hartija od vrednosti.
Emisioni kurs sa kojim akcije ulaze na tržište je inicijalni. Procena daljih kretanja na tržištu se vrši u odnosu na taj inicijalni emisioni kurs. Dakle, emisioni kurs akcija na primarnom tržištu je osnov sa kojim akcije počinju život na sekundarnom tržištu (Kočović, 2000).
Berzanski kurs akcija se, u zavisnosti od pretpostavki i primenjene metodologije može utvrđivati na različite načine, pa će u daljem izlaganju pažnja biti isključivo usmerena na metode i modele za utvrđivanje berzanskog kursa (tržišne cene) akcija.
Metodi za izračunavanje berzanskog kursa akcija
Metodi za izračunavanje berzanskog kursa akcija predstavljaju veoma široku i značajnu oblast savremene finansijske teorije, kojom su se bavili mnogi autori, tako da postoje vrlo različiti pristupi.
Utvrđivanje cena akcija je složenije od utvrđivanja cena obveznica. Tome doprinosi i činjenica da postoje dve karakteristike akcija koje predstavljaju glavnu smetnju i otežavaju analizu:
- prva se odnosi na nivo neizvesnosti, koji je mnogo veći kod akcija (naročito običnih), nego kod obveznica,
- druga karakteristika je što dividenda nije fiksna kao što je to slučaj sa kamatom. Ona se razlikuje u zavisnosti od rezultata poslovanja i varira od perioda do perioda. Međutim, u dugom roku vlasnici akcija očekuju njeno povećanje i to je jedan od njihovih osnovnih zahteva.
Postoji više metoda i načina za izračunavanje kursa akcija:
- analiza zasnovana na sagledavanju tokova sredstava,
- analiza zasnovana na sagledavanju dividendi,
- analiza prihoda i razvojnih mogućnosti i
- analiza zasnovana na sagledavanju prihoda.
Suština svih ovih metoda je u diskontovanju budućih prinosa, prihoda i dohodaka koji akcije donose svojim vlasnicima u periodu njihovog posedovanja. Metodi se razlikuju u pogledu toga šta treba diskontovati, ali ne postoji dilema oko procedure. Drugim rečima, ovo znači da se primenjuje sličan postupak kao kod izračunavanja vrednosti obveznica i drugih hartija od vrednosti, tj. da se vrši svođenje svih budućih prinosa hartija na njihovu sadašnju vrednost (Erić, Đukić, 2013).
Metodi zasnovani na analizi tokova sredstava
Metodi zasnovani na analizi tokova sredstava se zasnivaju na analizi
slobodnog cash flow-a tj. tokova sredstava (neto operativnog priliva). Na osnovu ovog načina kurs akcije se utvrđuje diskontovanjem svih budućih neto priliva sredstava (koji su jednaki razlici prihoda i troškova). Ako sa P označimo cenu akcije, k stopu kapitalizacije, Pr prihod, Tr troškove i CF neto tokove sredstava cenu akcije možemo izračunati iz sledeće jednačine:

Metod diskontovanja dividendi
Suštinu ovog metoda predstavlja posmatranje kursa akcija kao zbira sadašnjih vrednosti svih očekivanih budućih dividendi. Svođenje budućih vrednosti dividende na sadašnju vrednost se vrši pomoću diskontne stope (stope kapitalizacije) k koja odražava dve stvari:
- vremensku vrednost novca i
- rizik očekivanih budućih dividendi.
Berzanski kurs akcija korišćenjem ove metode može se izraziti kao:
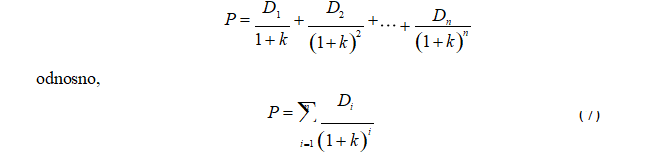
gde su:
Di - dividenda,
P - berzanski kurs akcije i k - diskontna stopa
![]()
i =1 (1 + k )i
Za formulu (7) možemo reći da predstavlja berzanski kurs akcije kao zbir svih očekivanih budućih prihoda koji će dobiti njeni vlasnici.
Postoje shvatanja da prilikom investiranja u obične akcije treba voditi računa da postoje, u zavisnosti od očekivanja, dve vrste ovih akcija i to:
akcije rasta, od kojih investitor očekuje više prihoda od budućeg rasta cena i akcije dohotka, od kojih investitor veće prihode očekuje kroz isplatu dividendi. Vlasnici akcija dobijaju dve vrste prihoda od posedovanja akcija:
- dividendu i
- kapitalni dobitak (gubitak), kao razliku između kursa po kome su akciju kupili i tekućeg kursa ili prodajne cene.
Ako uzmemo u obzir ova dva elementa, očekivani prinos (k) vlasnika akcije biće:

Prihod koji vlasnik akcije očekuje da ostvari se često naziva i tržišna stopa kapitalizacije. Za ilustraciju poslužićemo se jednostavnim primerom: Vlasnik je kupio akciju za 100 din, dividenda je 5 din, berzanski kurs akcije kroz godinu dana neka bude 110 din. Koliki je prinos investitora, tj. vlasnika akcije? Odgovor dobijamo korišćenjem jednačine (5), odnosno:
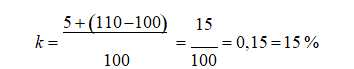
Iz jednačine (8) možemo izračunati sadašnju cenu akcije ukoliko znamo stopu prinosa investitora, koja je u stvari diskontna stopa (k). Sređivanjem jednačine (8) dobijamo da je sadašnji (tekući) berzanski kurs akcije (R0) jednak:
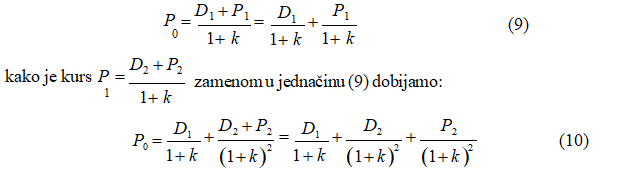
Sličnim postupkom možemo zameniti i P2 , pa kada i to uradimo dobijamo opštu formulu za izračunavanje berzanskog kursa akcija po metodu diskontovanja dividendi, tj. preko diskontovanja svih budućih dividendi uz uvažavanje kapitalnog dobitka (gubitka) kao elementa budućih prihoda.
Opšta formula data je sledećom jednačinom:
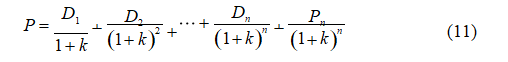
Kako idemo sve više budućnosti tako će se cena Pn sve više smanjivati, tj. približavaće se nuli i ako n ®¥ tada i Pn ® 0 . Uz uvažavanje ove primedbe jednačina (8) sada će izgledati:
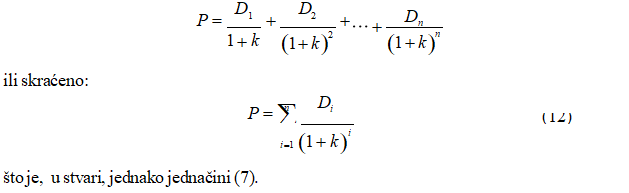
Jednačine (7) i (12) predstavljaju opšte teorijske formule za izračunavanje berzanskog kursa akcija. Međutim, problemi nastaju u momentu kada bi te formule trebalo upotrebiti. Osnovni problem se sastoji u promeni kretanja dividendi u budućnosti. Stope rasta dividendi nisu ni fiksne, ni jednake, niti vremenski ograničene, pa te činjenice opšte formule čine praktično neupotrebljivim ili vrlo teško upotrebljivim (Erić, Đukić, 2013).
Metodi rasta dividendi
Usled teške primenjivosti opštih formula metoda diskontovanja dividendi formulisana je grupa modela koji se zasnivaju na pretpostavci o rastu dividendi. Suština ove grupe metoda je da se dividenda posmatra kao rastuća kategorija, što ih čini realnijim (Welch, 2009). Pretpostavlja se da je dividenda u periodu t jednaka dividendi u prethodnom periodu t-1 uvećanoj po određenoj stopi rasta dividende g, tj. pretpostavlja se da važi relacija:
Dt = Dt -1 × (1+ g ) (13)
Iz ove relacije stopa rasta dividende može se izraziti kao:

Postoje tri modela rasta dividendi. Prvi od njih se zasniva na pretpostavci o nultom rastu dividende, tj. pretpostavlja se da dividenda neće rasti. U tom slučaju investitor, tj. vlasnik akcija očekuje isplatu konstantne dividende u budućnosti, odnosno važi relacija:
![]()
Iz ovoga možemo izvući zaključak da je stopa rasta dividende jednaka nuli (g=0), pa bi berzanski kurs akcije po ovom modelu bio:

I ovaj model ima ograničene mogućnosti korišćenja. Mogao bi se koristiti samo kada bi akcije isplaćivale fiksnu dividendu zauvek. Taj slučaj predstavlja, u stvari, i jedinu mogućnost njegove primene. Ovaj model se može koristiti pri izračunavanju berzanskog kursa preferencijalnih akcija, pa će metodologija dolaženja do obrasca (16) biti detaljnije obrađena u kada se bude govorilo o utvrđivanju njihovog berzanskog kursa.
Drugi model u okviru modela rasta dividendi se zasniva na ideji o konstantnom rastu dividendi. Naime, ovaj model polazi od pretpostavke da će dobitak, dividenda i berzanski kurs akcije uvek rasti po istoj stopi.
Ovaj model se u literaturi naziva Gordonov model, prema profesoru Myron Gordon-u.
Pretpostavimo da ulagač kupuje jednu akciju sa namerom da je drži godinu dana. Tekući berzanski kurs te akcije će se utvrditi kao zbir sadašnje vrednosti buduće dividende i berzanskog kursa akcije u trenutku prodaje:

gde je:
R0 - tekući berzanski kurs,
D1- iznos dividende koji će se primiti na kraju prve godine i P1 - berzanski kurs akcije na kraju prve godine.
Berzanski kurs akcije za drugog ulagača, koji je kupuje uz nameru da je drži, takođe, godinu dana može se utvrditi kao:

Za trećeg ulagača koji kupuje akciju berzanski kurs se može utvrditi kao:

itd. Pošto je P0 određeno sa D1 i P1, P1 sa D2 i P2 itd., berzanski kurs obične akcije bi se mogao izraziti jednačinom:
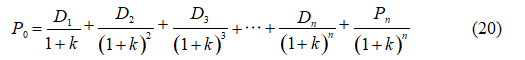
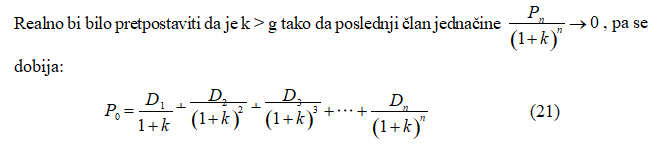
Iz formule (21) možemo zaključiti da je berzanski kurs običnih akcija funkcija dividende i primenjene stope kapitalizacije.
Ako se očekuja da u budućnosti dividenda konstantno raste po istoj stopi, iznos dividende koji će se primiti u bilo kojoj godini može se utvrditi kao:


Iz jednakosti (27) može se zaključiti da je kod modela konstantnog (normalnog) rasta dividendi berzanski kurs ( tržišna cena) običnih akcija određen iznosom dividende na kraju prve godine, tržišnom stopom kapitalizacije i stopom rasta dividende po akciji.
Očekivana stopa prinosa (tržišna stopa kapitalizacije) iz ovog izraza može se izračunati kao:

Iz jednakosti (28) vidimo da je očekivana stopa prinosa jednaka prihodu od dividende (dividend yield – izraz koji se često nalazi u izveštajima sa berze o kretanju sena akcija) i stope rasta dividende.
Za ilustraciju ovog modela poslužićemo se jednim prostim primerom.
Neka je npr. na kraju prve godine isplaćena dividenda po akciji 6 din, stopa rasta dividende po akciji 5%, a tržišna stopa kapitalizacije 11%. Korišćenjem ovog modela dobijamo da je berzanski kurs akcije:
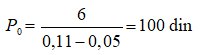
Ovaj model ima više realnosti od modela nultog rasta, ali mu je praktični značaj prilično mali.
U vezi sa tim treba napomenuti:
da se matematički rezultat u jednačini (24) zasniva na pretpostavci o konstantnom rastu dividende i konstantnoj diskontnoj stopi i
da bi cela analiza imala smisla neophodan uslov je da diskontna stopa bude veća od stope rasta dividende, tj. k > g. Ukoliko se stopa rasta dividende približava diskontnoj stopi sadašnja vrednost akcije neograničeno raste, a pri njihovoj jednakosti model je neupotrebljiv.
Treći model rasta dividende je model višestrukog rasta. Suština ovog modela je predviđanje rasta dividende u budućnosti, što celokupnoj analizi cena akcija daje mnogo veću realnost. Umesto rasta dividende po konstantnoj stopi g u ovom modelu se pretpostavlja da će dividenda rasti po različitim stopama g1, g2, g3, ... , gn tokom vremena. Pretpostavka je logična, pošto se često dešava da dividende na akcije novih firmi u fazama razvoja brže rastu da bi kasnije, kada firme uđu i fazu zrelosti stope rasta počele da stagniraju, pa čak i da opadaju (Erić, Đukić, 2013).
Formula za izračunavanje berzanskog kursa akcija metodom višestrukog rasta dividende može biti veoma složena, u zavisnosti od toga koliko stopa rasta uzimamo u model. Radi pojednostavljenja uzećemo slučaj u kome imamo samo dvostruki rast dividendi – po stopama g1 i g2. Pretpostavićemo još da od perioda 0 do perioda T dividende rastu pa stopi g1, a posle tog perioda po stopi g2. Rast dividendi u tom slučaju će izgledati:
![]()
![]()
Iz ovoga vidimo da postoje dva toka dividendi. Uz uvažavanje takve realnosti neophodno je odrediti njihovu sadašnju vrednost koristeći jednačinu (23) kao polaznu osnovu. Uvođenjem jednakosti (29) i (30) u jednačinu (23) dobijamo:
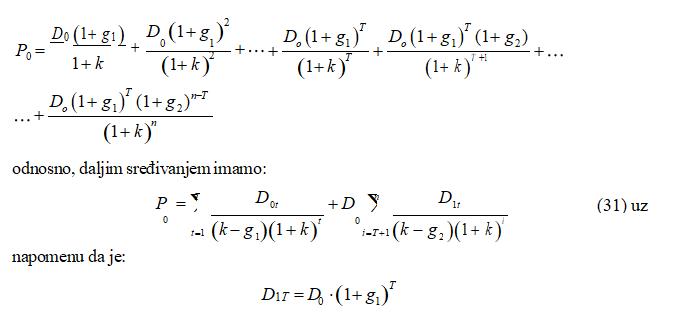
Ovde je prikazan slučaj u kome postoje samo dve faze rasta dividende. Naravno, postoji i mogućnost definisanja i širih verzija ovog modela, sa tri ili četiri faze u rastu dividendi, čime se uvažava pretpostavka da se stope rasta menjaju više puta.
Određene probleme u korišćenju ovog modela može prouzrokovati procena parametara g i
k. Stope rasta dividendi se mogu proceniti na osnovu podataka o kretanju prihoda, akumulacije i investicija. Što se tiče procene tržišne stope kapitalizacije tu je problem teže prirode i rešava se, uglavnom, slobodnom procenom vodeći računa o visini kamatne stope i stope inflacije uz uvažavanje iskustva drugih (Kočović, 1999).
Na kraju treba reći da je korišćenje ove metode danas značajno olakšano, s' obzirom na to da postoje razvijeni programi kojima se lako mogu simulirati različita kretanja bitnih parametara i veličina.
Razlike između tri pomenuta metoda rasta dividendi mogu se prikazati i grafički, što se može videti na slici.
Metodi zasnovani na sagledavanju prihoda
Ovu grupu pristupa određivanja cena akcija čine oni metodi koji u analizi polaze od sagledavanja prihoda a ne dividende. Veza između prihoda i dividende je očigledna, pošto je:
dividenda = prihod – zadržani profit (akumulacija)
Za veličinu prihoda uzima se prihod po jednoj akciji (EPS – earnings per share), koji se dobija kada se podeli ukupan prihod firme i broj emitovanih akcija.
Ukoliko bi se ceo prihod isplatio u obliku dividendi (ovo je veoma redak slučaj i u njemu bi važila jednakost D = EPS, a za takve firme se kaže da su "krave muzare"), formula za izračunavanje tržišne cene akcija bi glasila:

Ovo je najprostiji slučaj, sa nultim rastom EPS - prihoda po akciji.
U praksi firme gotovo nikada ne isplaćuju ceo prihod kao dividendu. S' obzirom na to da svaka firma ima određene planove rasta i razvoja jedan deo prihoda se zadržava na ime akumulacije u obliku zadržanog profita. On se posmatra kao generator razvojnih mogućnosti i ima svoju sadašnju vrednost i cenu. Npr. ako firma prihvati novi ivesticioni projekat sa pozitivnom neto sadašnjom vrednošću to će dovesti do povećanja cena njenih akcija. Uključivanjem razvojnih mogućnosti u jednakost (32) dobijamo da je tržišna cen aakcije jednaka:

gde je SVRM - sadašnja vrednost razvojnih mogućnosti preudzeća.
Da bi došlo do povećanja berzanskog kursa akcija neophodno je da budu zadovoljena najmanje dva uslova:
- prihod mora biti stvarno zadržan u obliku akumulacije i
- investisioni projekat kojim se realizuju razvojne mogućnosti mora imati pozitivnu neto sadašnju vrednost, što drugim rečima znači da mora donositi prihod veći od troškova kapitala neophodnog za njegovo finansiranje.
Metodi zasnovani na korišćenju P/E racija
Kod ovog metoda za izračunavanje berzanskog kursa akcija polazi se od R/E racija, tj proporcije tekućih tržišnih cena i prihoda po akciji.
Ukoliko jednačinu (33) uzmemo kao polaznu osnovu i ako obe strane podelimo sa EPS dobijamo izraz za R/E racio:
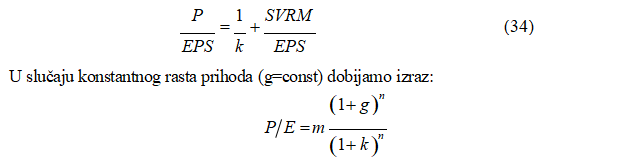
odnosno, posle skraćivanja imamo:

R/E racio je vrlo važan pokazatelj za svaku firmu. On se koristi kao mera za poređenje sa drugim firmama koje mogu biti slične ili koje posluju u istoj grani. R/E je termin koji svakodnevno operiše na berzi akcija. Nalazi se u svim dnevnim kotacijama i izveštajima sa berze. On se izračunava iz odnosa tekućeg berzanskog kursa akcija i prihoda po akciji. Na njega utiču sledeće veličine: stopa prinosa investitora, tj.diskontna stopa (k), stopa rasta dividendi (g), povećanje prihoda po akciji (EPS), dužina vremenskog perioda itd. Manja diskontna stopa, veće stope dividende i prihoda kao i duži vremenski period su faktori koji povećavaju R/E racio. Visok R/E racio ne znači da se automatski radi o kvalitetnijim firmama. Za sagledavanje uspešnosti firme neophodna je šira analiza i uključivanje drugih aspekata – razvojnih perspektiva menadžmenta i menadžera, analiza konkurentske pozicije, finansijska analiza itd.
R/E racio može biti visok iz sledećih razloga:
- zato što su cene akcija suviše visoke,
- zato što je prihod suviše mali ( u slučaju da je prihod jednak nuli R/E racio bi bio beskonačna veličina),
- zato što je diskontna stopa suviše niska i
- zbog postojanja različitih računovodstvenih metoda.
Upoređenje R/E racija je jedan od veoma popularnih metoda za izračunavanje berzanskog kursa akcija. Da bi se mogao uspešno koristiti neophodno je detaljno poznavanje njegovih osnovnih karakteristika što, uostalom, važi i za sve ostale metode.
Međutim, treba istaći da korišćenje pojedinih metoda u velikoj meri zavisi od razvojne faze u kojoj se preduzeće nalazi. Ovde se misli na faze u kretanju finansijskih parametara, ako što su dividenda i prihod.
Možemo razlikovati tri faze:
- fazu rasta, u kojoj dolazi do rasta preduzeća, povećanja profitabilnosti, profitnih margina, rasta prihoda i EPS. Ovu fazu karakteriše rast svih stopa.
- tranzitornu fazu, u kojoj dolazi do saturacije proizvoda i tržišta, do smanjivanja stopa rasta i profitnih margina,
- fazu zrelosti, gde se stabilizuju veličine EPS, ROI (Damodaran, 2015) ( prinos na investicije), dividende i sl.
Imajući u vidu ove tri faze za uspešno korišćenje metoda za određivanje berzanskog kursa akcija treba uzeti u obzir više faktora:
- sagledati očekivani rast dividende u narednih pet godina,
- stope rasta prihoda i akumulacije na početku tranzitorne faze,
- vek trajanja tranzitorne faze,tj. broj godina do faze zrelosti,
- proceniti rast EPS u tanzitornoj fazi,
- nepraviti grube procene rasta EPS, ROE ( stopa prinosa na sopstvena sredstva), akumulacije i drugih veličina u fazi zrelosti (Damodaran, 2015).
Utvrđivanje berzanskog kursa akcija je izuzetno kompleksna oblast u kojoj postoji dosta faktora koje treba obuhvatiti. Takođe, karakterističan je visok stepen međuzavisnosti između njih, pre svega između prihoda i dividende, diskontne stope, stope rasta prihoda i dividende, vremenskog perioda i sl.
Nominalni, emisioni i berzanski kurs preferencijalnih akcija
Kao i sve ostale hartije od vrednosti, tako i preferencijalne akcije imaju svoj nominalni, emisioni i berzanski kurs.
Iznos na koji glasi preferencijalna akcija predstavlja njen nominalni kurs. To je, u stvari , utvrđen iznos koji treba da se isplati preferencijalnim akcionarima u slučaju likvidacije preduzeća. Dividenda se može utvrditi kao procenat od nominalne vrednosti, npr. 7% u odnosu na nominalnu vrednost od 100 din, ali se najčešće utvrđuje u apsolutnom iznosu, a to je u ovom primeru 7 dinara.
Kurs po kome se ove akcije emituju na primarnom tržičtu hartija od vrednosti predstavlja njihov emisioni kurs, a to je , u stvari cena po kojoj će prvi kupci kupiti tu akciju da bi je kasnije preprodali. Na visinu ovog kursa utiče i visina spreda i ažija, odnosno disažija.
Pošto se radi o permanentnom ulaganju, koje obezbeđuje fiksni godišnji iznos dividende i pošto preferencijalne akcije nemaju, kao ni obične akcije, konačan rok dospeća za utvrđivanje njihovog berzanskog kursa primenjuje se formula (15) koja je identifikovana kao formula za određivanje berzanskog kursa akcija sa nultim rastom dividende. Koristeći pomenutu formulu kao polaznu osnovu imamo:
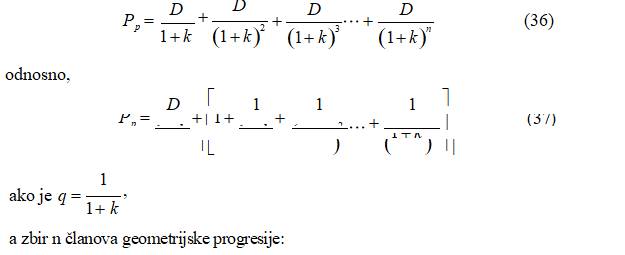

Izraz (38) identičan je izrazu (16) i predstavlja formulu po kojoj se
izračunava berzanski kurs preferencijalnih akcija. Vidimo da se on dobija kada se podeli konstantni godišnji iznos preferencijalne dividende sa primenjenom tržišnom stopom kapitalizacije.
Ako, npr. preduzeće emituje preferencijalne akcije nominalne vrednosti 100 din, uz nominalnu dividendnu stopu od 10%, njihov berzanski kurs biće jednak nominalnom samo ako je tržišna stopa kapitalizacije jednaka nominalnoj dividendnoj stopi. Koristeći formulu (38) imamo:
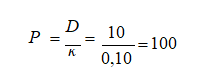
Pošto će ulaganje u preduzeće koje se razvija i raste biti manje rizično to će usloviti sniženje tržišne stope kapitalizacije. Ako pretpostavimo sniženje ove stope na, recimo, 8% berzanski kurs ovih akcija će porasti na 125 din (10 : 0,08).
Ukoliko se, pak, uslovi poslovanja preduzeća pogoršavaju, porašće rizik ulaganja u preduzeće, što će usloviti porast tržišne stope kapitalizacije, odnosno pad tržišne vrednosti preferencijalnih akcija. Ako pretpostavimo da je ova stopa porasla na 12%, berzanski kurs ovih akcija će se smanjiti na 83,33 din (10 : 0,12).
Zaključak
Utvrđivanje nominalnog, emisionog i berzanskog kursa predstavlja veoma široku i značajnu oblast savremene finansijske teorije kojom su se bavili mnogi autori, pa otuda i ne čudi to što postoji veliki broj metoda i postupaka za utvrđivanje, cene (kursa) hartija od vrednosti na finansijskom tržištu kratkoročnih i dugoročnih hartija od vrednosti (koja su segmenti tržišta novca, odnosno tržišta kapitala).
U radu je pokazano da je utvrđivanje nominalnog, emisionog i berzanskog kursa naučno utemeljeno, sa razrađenom metodologijom i da ima čvrste korene u finansijskoj matematici, kao primenjenoj ekonomskoj disciplini u okviru finansijskog menadžmenta.
Takođe, prikazan je celokupan metodološki proces iznalaženja nominalnog, emisionog i berzanskog kursa hartija od vrednosti na finansijskom tržištu.
Suština svih prikazanih metoda je u diskontovanju budućih prinosa, prihoda i dohodaka koji hartije od vrednosti donose svojim vlasnicima u periodu njihovog posedovanja.
Metodi se razlikuju u pogledu toga šta treba diskontovati, ali ne postoji nikakva dilema oko procedure. Drugim rečima, ovo znači da se primenjuje sličan postupak i kod utvrđivanja vrednosti i dugoročnih i kratkoročnih hartija od vrednosti, tj. da se vrši svođenje svih
budućih prinosa hartija od vrednosti na njihovu sadašnju vrednost.
Pokazalo se da je utvrđivanje berzanskog kursa izuzetno kompleksna oblast u kojoj postoji dosta faktora koje treba obuhvatiti.
Takođe, karakterističan je visok stepen međuzavisnosti između faktora koji deluju na formiranje kursa dugoročnih hartija od vrednosti, pre svega između kamatne i diskontne stope, prihoda i dividende, stope rasta prihoda i dividende, vremenskog perioda i sl.
Osim nabrojanih faktora na formiranje berzanskog kursa utiče i čitav niz drugih elemenata, koji su, uglavnom, sadržani u formiranju ponude i tražnje za hartijama od vrednosti na sekundarnom tržištu hartija od vrednosti.
4 U stručnoj literaturi koja tretira ovu problematiku akcije narednih emisija se nazivaju još i mlade akcije ili ''mladice''.
Reference
2.Damodaran, A. 2015. Applied Corporate Finance, 4th Edition. John Wiley & Sons.
3.Erić, D., & M. Đukić. 2013. Finansijska tržišta i instrumenti u uslovima krize. Institut ekonomskih nauka. Beograd.
4.Ivaniš, M., &S. Nešić. 2011. Poslovne finansije. Univerzitet Singidunum. Beograd.
5.Kočović, J. 2000. Utvrđivanje nominalnog, emisionog i berzanskog kursa akcija. Jugoslovensko bankarstvo. br. 5-6.
6.Krasulja, D., & M. Ivanišević. 2007. Poslovne finansije. Ekonomski fakultet. Beograd.
7.Kočović, J. 2009. Finansijska matematika. Ekonomski fakultet. Beograd.
8.Kočović, J. 1999. Metodološke osnove utvrđivanja nominalnog, emisionog i berzanskog kursa obveznica na rentnom tržištu. Bankarstvo. br. 11/12.
9.Milojević, I., & R. Tepavac. 2010. Finansijska vrednost sopstvenog kapitala akcionarskog društva. Poslovna politika. br. 7-8.
10.Poslovni leksikon, Velarta, Beograd, 2009.
11.Welch, I. 2009. Corporate finance: an introduction. Pearson Education. Boston.
Objavljeno u
God. 3 Br. 3 (2017)
Ključne reči
🛡️ Licenca i prava korišćenja
Ovaj rad je objavljen pod Creative Commons Attribution 4.0 International (CC BY 4.0).
Autori zadržavaju autorska prava nad svojim radom.
Dozvoljena je upotreba, distribucija i adaptacija rada, uključujući i u komercijalne svrhe, uz obavezno navođenje originalnog autora i izvora.
Zainteresovani za slična istraživanja?
Pregledaj sve članke i časopise