Najbitniji sistem za upravljanje rizicima i merenje finansijski performansi jeste rejting sistem. Rejting sistem se smatra integralnim delom bankarskih tekućih poslova i njihove kulture upravljanja rizicima. Sve banke se trude da istaknu tu njegovu pripadnost tekućim poslovima, kako bi pokazali supervizorima neophodnost njegovog korišćenja u svrhu determinisanja zahteva minimalnog regulatornog kapitala.

Komitet u Bazelu za pojedine klase izloženosti rizicima, preporučuje korišćenje osnovne metodologije kod koje bankarske institucije kao ulaznu veličinu koriste sopstvenu procenu rizika neplaćanja dužnika, dok se procene dodatnih faktora rizika primenjuju putem standardizovonih pravila supervizora.

Ova osnovna metodologija je dostupna za bankarske institucije koje imaju mogućnost da svoje supervizore uvere da su one sposobne da odgovore na određene minimalne zahteve bankarskog sistema, proces upravljanja rizika i sposobnost procene njegovih bitnih komponenti.

Takođe pored osnovne metodologije definisane su i napredne metodologije koje pružaju mogućnost unutrašnje procene komponenti rizika. Široka primena navedenih procena je važan deo dinamičkog i risk-senzitivnog IRB pristupa (Internal Rating Based). Tako mogu da se identifikuju i razlikuju one bankarske institucije koje imaju sposobnost da sprovedu određenu validnu i kvantifikovanu procenu rizika.

Neki određeni modeli, postupci i procesi procene verovatnoće neplaćanja u određenim situacijama, putem dobijenih rezultata, omogućuju menadžmentu bankarskih institucija detaljno analiziranje realne slike mogućih dužnika što u krajnjem pruža i moguću bolju analizu njihovog difolta.

Uvod

Osnovnu bazu determinisanja rejtinga izloženosti riziku ili rejtinga drugih ugovornih strana kod manjeg broja bankarskih institucija, a u okviru određenih portfolia, činio je postupak verovatnoće ispunjenja obaveza ili drugi kvantitativni alati.

Takvi postupci trebalo bi da imaju mogućnost da budu razvijeni od strane isporučioca (vendor) i uglavnom pored kvalitativnih i kvantitativnih faktora (finansijske proporcije), sadrže i stadardizovane faktore (istorija plaćanja, kreditni izveštaji itd). (Bessis J, 2019)

Ovakve alate kod velike korporativne izloženosti, primenjivalo je mali broj bankarskih institucija, dok je nekoliko njih koristilo ove alate u situacijama srednjeg tržišta ili korisnika iz malog biznisa. Kao primer za navedenu situaciju može se navesti korišćenje kreditnih skor modela (kategorije

„scorecard”, modele difolta, isporučioca (vendor) i konsultanata).

Takođe navedeni modeli imaju u sebi bitne elemente u postupcima procene rizika u velikom broju institucija. Kod konstruisanja banaka, prvo se definišu finansijske zavisne varijable, koje se pojavljuju prilikom pružanja informacionih podataka o procentu verovatnoće neispunjenja obaveza.

Putem uzorka razmatranog kredita, a primenom dostupnih istorijskih podataka, bankarska institucija procenjuje uticaj svake od ovih zavisnih varijabli na postupak neispunjenja obaveza. Utvrđenih koeficijenti procene se dalje koriste na podatke trenutnih zajmova i pojavljuju kao rezultat koji je utvrđen u proceni pitanja procenta verovatnoće neispunjenja obaveza. Rezultat se zatim konvertuje u rejting stepen (realni inputi kod takvih modela su vrlo identični kvantitativnim elementima rizika, utvrđenog od strane procenitelja).

Aktivnosti i procesi koji počivaju na statističkim modelima imaju bitniju ulogu kod manjih korporativnih zajmova nego na tržištima srednje veličine ili kod velikih korporacija.

Pojedine bankarske institucije su zasnovale svoje rejtinge isključivo na statističkim skor modelima difolta i kredita ili specijalnim ciljevima finansijskih analiza, ne uzimajući u obzir jednostavne mehaničke procese. Takci rejtinzi omogućuju dodeljivanje rejtinga radi podešavanja rejtinga na određeni unapred ograničeni stepen koji počiva na faktorima procene. (Brealey R., 2021)

U određenoj situaciji definisanog procesa scorecard definiše stepen, dok procenitelj po ličnoj analizi, može definisati finalni stepen naniže ili naviše i to maksimalno za jedan ili dva stepena.

Pored toga, kvantitativnim i faktorima procene se mogu dodeliti maksimalni poeni što efikasno ograničava uticaj razmatranja određene procene na konačni rejting. Skoro 20% bankarskih institucija primenjuje ovaj koncept u svojim velikim korporacijama, dok se identičan procenat institucija izjasnio da primenjuje ovaj koncept za svoje manje korporacije i srednja tržišta. Stavljanje ograničenja na proceni je profesionalnije kada se te procene isključivo primenjuju za rast rejtinga, a ne za njegov pad. Najveći broj institucija rejtinge dodeljuje primenom najznačajnijih delova procene, gde je relativna značajnost ukazana delovima koji nisu ograničeni.

Regresiona analiza

U statističkom modeliranju, regresiona analiza predstavlja proces statističkih analiza na osnovu kojih se vrši vrednovanje uzajamne povezanosti zavisne ili kriterijumske promenljive i nezavisnih (predikatorskih) promenljivih. (Matz L., 2017)

Dobijeni rezultati na osnovu regresione analize ističu da se vrednosni podatak zavisne promenljive menja sa promenom vrednosnog podatka neke nezavisne promenljive, dok ostali vrednosni podaci nezavisnih promenljivih ostaju nepromenjeni.

Kao stalan zadatak regresione analize pojavljuje se aproksimacija regresone funkcije, pomoću koje se ističe veza između promenljivih zavisnih i nezavisnih. Ova analiza se pored toga koristi i za vrednovanje funkcionalne zavisnosti izmedju pomenutih promenljivih, kao i prirodu tih zavisnosti.

U praksi nas može recimo zanimati zavisnost između zarada zaposlenih i njihovog obrazovanja, stopa i to kamatnih i ponude novca. Da bi se utvrdilo da li postoji zavisnost između određenih pojava i u kojoj meri je njihova zavisnost, neophodno je primeniti određeni model regresije.

Analiza regresije se primenjuje u dve totalno različite svrhe. Najpre se primenjuje za planiranje, prognoziranje i moguće predviđanje, u situacijama u kojima se njeno korišćenje poistovećuje se poljem mašinskog učenja. Zatim se koristi i u situacijama za utvrđivanje uzročno posledičnih veza između zavisnih i nezavisnih promenljivih.

Da bi se uspešno koristila ova vrsta analize za predviđanje, lice koje istražuje treba da oprezno definiše i objasni postojanje uzročne posledične veze između promenljivih odnosno njihovu funkcionalnu vezu. Funkcionalna veza je naročito važna u situacijama u kojima istraživači imaju mišljenje da će se za procenjivanje uzročno posledične veze koristiti samo podaci iz uzorka ili statističkog skupa i odgovarajuće funkcionalne relacije.

Regresiona analiza u finansijskim institucijama

Ključna prednost regresionih modela u finansijskim institucijama je njihova sposobnost  da  analiziraju  složene  veze  između  promenljivih  i  pruže kvantitativne procene koje podržavaju donošenje utemeljenih poslovnih odluka. (Gitman L., 2019)

Ulazne karakteristike koje nisu značajne za model mogu ozbiljno narušiti kvalitet i stabilnost modela kada se koriste radi predviđanja dužničkog rizika u vezi sa ovim podacima. Poželjno je da se promenljive, koje nemaju veliki uticaj na rezultate modela, jednostavno ignorišu i time pojednostavi model, što u svakom slučaju licima koja vrše regresionu analizu olakšava rad.

Način da se ponesemo sa ovim problemom se nalazi u podeli uzroka na dva dela, gde se jedan deo (uzorak obuke) koristi radi procene modela a drugi deo je hold-out uzorak (ostatak uzorka) koji se koristi kod validacije rezultata.

Konzistentnost rezultata oba uzorka se jednovremeno uzimaju kao indikatori stabilnosti modela.

U finansijskim institucijama regresiona analiza se najčešče se koristi u sledećim slučajevima:

a)  Kreditna analiza: Regresijski modeli se koriste za procenu kreditnog rizika klijenata. Modeli poput logističke regresije se koriste za predviđanje verovatnoće da će klijent otplaćivati kredit redovno.

b)  Upravljanje aktivom i pasivom: Finansijske institucije koriste regresione modele za predviđanje nivoa depozita i kredita, što im pomaže u upravljanju svojim bilansom i rizicima povezanim sa likvidnošću.

c)  Marketinške strategije: Regresiona analiza se koristi za identifikovanje najisplativijih segmenata klijenata i utvrđivanje najdelotvornijih marketinških kanala i kampanja.

d)  Prevencija prevare: Regresioni modeli se koriste za otkrivanje sumnjivih transakcija i obrazaca ponašanja koji mogu ukazivati na prevaru.

e)  Prilagođavanje cena: Banke koriste regresione modele za određivanje optimalnih kamatnih stopa i naknada zasnovanih na tržišnim uslovima i profilu rizičnosti klijenata.

f)  Upravljanje rizicima: Regresioni modeli se koriste za procenu kreditnog, tržišnog i operativnog rizika kojem je banka izložena.

Analiza diskriminante

Analiza diskriminante se vrši na sličan način kao u kod linearnog regresionog modela.

Zapravo proporcije između koeficijenata regresionog modela su jednake sa odgovarajućim proporcijama analize diskriminante. Razlika između ova dva metoda je teorijska: dok u regresionom modelu karakteristike imaju determinističku prirodu, a stanje difolta je slučajna promenljive. Kod analize determinante je sasvim suprotno tj. karakteristike predstavljaju slučajnu promenljivu dok je stanje difolta determinisano. Ove su razlike u praksi virtuelno nevažne.

Možemo zaključiti da su prednosti i mane analize diskriminante putem ovog modela slične onima kod regresionog modela, a to su:

– Analiza diskriminante je široko poznata metoda sa algoritmima procene koji su raspoloživi;

– Kada se jednom koeficijenti procene tada rezultati mogu da se obračunaju direktno kao linearne funkcije;

– Pošto se karakteristike Xi realizuju na osnovu slučajnih promenljivih tada se statistički testovi značajnosti modela i koeficijenata baziraju na pretpostavkama multivarijantne normalnosti. Ovo je međutim nerealno kod promenljivih koje se tipično koriste u modelima rejtinga, kao na primer, kod finansijskih proporcija dobijenih na osnovu bilansa. Stoga su metode analize stabilnosti modela i mogućnosti koeficijenata ograničene u poređenju između uzorka i ostatka uzorka; i

– Apsolutne vrednosti funkcije diskriminante se ne mogu interpretirati po nivoima.

Jedan mogući način dobijanja homoshedastičnih veličina predstavlja izračunavanje procenjenih veličina putem metode najmanjih kvadrata sa težinama (WLS). Iako je ovo moguće to i nije česta praksa zbog toga što, u cilju dobijanja učestalosti difolta, podaci moraju biti grupisani pre izvršenja procene. (Greuning H., 2018)

Grupisanje uključuje značajne praktične probleme kao što su određivanje veličina i broja grupa i način tretmana različitih kovarijanti unutar jedne jedine grupe (Zhou et al., 2024).

Logit i Probit modeli predstavljaju bolji način procene jer ne zahtevaju prethodno grupisanje kao u ML metodu (to je metod maksimalne verodostojnosti - verovatnoće). Kod binomno zavisnih promenljivih funkcija verovatnoće glasi:

Kod probit modela funkcija P predstavlja funkciju normalnog rasporeda verovatnoćaa u Logit modelu ona predstavlja logaritamsku funkciju rasporeda verovatnoća. Putem ove jednačine procena modela je teoretski ubedljiva i jednostavna za rukovanje. (Samuels J., 2016)

Nadalje, ovakav ML pristup nas vodi do širokog seta testova radi evaluacije modela i njegovih promenljivih. Obično se izbor link funkcije ne zasniva na teorijskoj osnovi. Korisnici kojima je bliža upotreba normalnog rasporeda verovatnoća opredeliće se za Probit model.

I stvarno, razlike u rezultatima po obe klase modela su često zanemarljive. To je zbog toga što obe funkcije imaju slične forme osim tail-ova, koje su teže za obračunavanje kod Logit modela. Istina je da je Logit model lakši za rukovanje jer je lakše obračunavanje estimatora (procenitelja).

Međutim složenost proračunavanja danas je često beznačajna pošto najveći broj korisnika upotrebljava statističke softverske pakete gde su algoritmi procene integrisani u softverska rešenja. Važna je i činjenica da se koeficijenti Logit modela mogu lakše interpretirati (Ochuba et al., 2024).

Da bismo to razumeli tranformisaćemo Logit model dat jednačinom (1) na sledeći način:

Na levoj strani jednačine (2) nalaze se odnosi između verovatnoće difolta i verovatnoće preživljavanja (survival).

Sada se lako može videti da varijacija jedne promenljive xi u jednoj jedinici ima učinak koji je jednak  na verovatnoću kada veličina βk koeficijent promenljive xi.

Transformisani koeficijent e^β se zove odnos verovatnoće (adds-ratio). On predstavlja multiplicirani učinak karakteristika dužnika na verovatnoću. Stoga u Logit modelu koeficijent se može interpretirati na verovatan način što nije slučaj u Probit modelu.

Panelni modeli

Do sada opisane metode predstavljaju poprečne metode zbog toga što se sve promenljive odnose na isti vremenski period. Finansijske institucije tipično raspoređuju setove promenljivih na više od jednog perioda kod svakog dužnika. U ovom slučaju moguće je proširiti poprečne inpute podataka na panelske setove podataka.

Na taj način povećavamo broj raspoloživih posmatranja kod procenitelja a takođe povećavamo stabilnost i preciznost rejting modela. Panelni modeli mogu integrisati u sebe i makroekonomske promenljive.

Makroekonomske promenljive mogu poboljšati model iz nekoliko razloga. Najpre mnogi izvori makroekonomskih podataka su ažurniji i dostupniji od mezo i mikro podataka, jer podatke o makroekonomskim promenljivim objavljuje zvanična nacionalna statistika. Na primer, finansijski odnosi obračunati po osnovu bilansnih informacija obično se ažuriraju na godišnjem nivou i nisu stariji od dve godine kada ih koristimo radi procene rizika. (Dowling E.T., 2017)

Cene nafte na primer, su nam na raspolaganju po dnevnoj učestalosti podataka, isto tako cene plemenitih metala, cene akcija na berzama i slično menjaju se više puta u toku dana i mi te informacije možemo dobiti.

Naglašavanjem makroekonomskih inputa u modelu možemo koristiti radi formiranja stress testova kreditnog rizika. Pošto makroekonomske promenljive primarno utiču na apsolutne vrednosti verovatnoća difolta, razumno je inkorporirati makroekonomske impute u ove klase modela kod procenjivanja verovatnoće difolta. (Engeimann B., at.all. 2018)

Na prvi pogled panelni modeli su slični presečnim modelima. Ustvari, mnogi razvojni programeri zanemaruju dinamički obrazac promenljivih i jednostavno ih uključuju u Logit i Probit model. (Alastair L., 2022)

Generalno uzevši poprečni podaci ispunjavaju ovakve zahteve ali panelski podaci ne ispunjavaju iste zahteve, i to stoga što posmatranja istog perioda i posmatranja istog dužnika mogu biti u korelaciji. Uvođenje korelacije u procedure procene je komplikovano. (Mishkin F., 2020)

Na primer, estimator sa fiksnim učinkom koji nam je poznat iz analize panela kod neprekidne zavisne promenljive nije na raspolaganju u Probit modelu. Pored toga, modifikovani estimator sa fiksnim efektom u Logit modelu isključuje sve dužnike koji nisu u difoltu iz analize pa nam se zbog toga čini kao da je neodgovarajući. Na kraju, estimatori sa slučajnim efektom koji su propisani u literaturi mogu biti obračunati samo po osnovu upotrebe specijalizovanih softverskih paketa.

Modeli hazarda

Svi modeli koji su do sada navedeni pokušavali su da ocene rizičnost dužnika putem procenjivanja određenog tipa ili rezultata koji bi indikovao da li dužnik jeste ili nije sklon difoltu unutar specifičnog horizonta predviđanja.

Međutim, nije izvedeno ni jedno egzaktno predviđanje difolta u vremenu. Pored toga ovakvi pristupi ne omogućavaju evaluaciju dužnikovog rizika u budućnosti koji ne bi ušao u difolt u toku jednog referentnog vremenskog perioda.

Ovi nedostaci se mogu prevladati pomoću modela hazarda, koji eksplicitno obrađuje funkciju preživljavanja i sledstveno tome vreme u kome uzimamo u obzir dužnički difolt.

Unutar ove klase modela Coxov proporcionalni model hazarda je najzastupljeniji regresioni model pošto on nije zasnovan na bilo kakvim pretpostavkama koje razmatraju prirodu ili oblik osnovne distribucije preživljavanja.

Model ocenjuje da je utemeljena stopa hazarda (pre nego vreme preživljavanja) funkcija nezavisne promenljive. Ne čini se nikakva pretpostavka o prirodi ili obliku funkcije hazarda. Stoga je Coxov regresioni model ustvari semiparametarski model.

On se može opisati kao: hi(t/xi)= h0(t) × (3) , gde veličina hi(t/xi)

označava rezultirajući hazard koji je zadat prema kovarijatima kod respektivnog dužnika u respektivnom periodu preživljavanja t.

Izraz h0(t) se naziva osnovna linija hazarda i predstavlja hazard kada su sve nezavisne promenljive jednake nuli. Ako se kovarijati mere kao devijacije u odnosu na njihove respektivne srednje vrednosti tada veličina h0(t) može biti interpretirana kao stopa hazarda po nekom prosečnom dužniku. Model koji je gore prikazan sadrži važne pretpostavke. Najpre on specificira višestruki odnos između funkcije hazarda i logaritamske linearne funkcije zavisne promenljive koja ukazuje da odnos hazarda kod dva dužnika ne zavisi od vremena tj. da je relativna rizičnost dužnika konstantna odakle potiče ime za Coxov proporcionalni model hazarda.

U ovom modelu se pretpostavlja da je tačka difolta u vremenu neprekidna slučajna promenljiva. Međutim, često se dešava da se finansijski uslovi dužnika ne posmatraju kontinelno (neprekidno) već kao diskretne vrednosti u vremenu. Štaviše, kovarijati su tretirani kao da su konstantni u vremenu dok se, tipične zavisne promenljive kao što su, na primer finansijski odnosi, menjaju tokom vremena.

Iako postoje neki napredniji modeli koji sadrže gore pomenute osobine procena u ovakvim modelima postaje kompleksna.

Prednosti i mane modela hazarda mogu se sumarno prikazati kao (Alirezaie et al., 2024):

-  Modeli hazarda omogućavaju procenu funkcije preživljavanja za sve dužnike. Vremenski period istorijskih podataka o difoltu je osnova za procenu preživljavanja dužnika i verovatnoću difolta u narednom vremenskom periodu i

-  Ovi modeli indirektno procenjuju realne pretpostavke o difoltu u budućem vremenskom periodu.

Neuronske mreže

Neuronske mreže su vrsta računarskog sistema inspiriranog strukturom i funkcijama bioloških neuronskih mreža u mozgu. Glavne komponente neuronskih mreža su (Abrahams et al., 2024a):

-  Arhitektura mreže - Sastoji se od međusobno povezanih "čvorova" ili "neurona" koji obrađuju informacije. Najčešće imaju ulazni, skriveni i izlazni sloj.

-  Učenje - Neuronske mreže uče iz podataka, automatski otkrivajući obrasce i karakteristike, dok se parametri veza između neurona podešavaju tokom procesa učenja.

-  Nelinearnost - Sposobnost da modeliraju kompleksne, nelinearne odnose između ulaza i izlaza.

-  Paralela s biološkim mozgom - Slično kao biološke neuronske mreže, veze između neurona imaju "snagu" koja se prilagođava tokom učenja.

-  Primena - Koriste se za zadatke raspoznavanja uzoraka, predviđanja, klasifikacije i sl. Primenjuju se u raznim domenama kao što su obrada prirodnog jezika, robotika, itd.

-  Neuronske mreže predstavljaju moćan alat mašinskog učenja kojim može spoznati i modelirati kompleksne odnose među podacima. Intenzivno se istražuju i imaju široku primenu u savremenoj informatici i tehnologiji.

Primena neuronskih mreža u finansijskom sektoru ima veliki značaj od kojih su najvažnije:

Otkrivanje prevare: Neuralne mreže mogu analizirati velike količine podataka o transakcijama kako bi identifikovale obrasce lažnih aktivnosti, kao što su neobično ponašanje u potrošnji ili sumnjive transakcije. Ovo pomaže finansiskim institucijama da efikasnije otkriju i spreče prevare.

Procena kreditnog rizika: Neuronske mreže mogu analizirati kreditnu istoriju, prihode i druge finansijske podatke kako bi procenile kreditnu sposobnost podnosilaca zahteva za kredit. Ovo omogućava finansijskim institucijama da donose preciznije kreditne odluke zasnovane na dobijenim podacima.

Modeliranje ponašanja kupaca: Neuronske mreže se mogu koristiti za analizu podataka o klijentima, kao što su istorije transakcija i obrasci pregledanja, da bi se bolje razumelo ponašanje i preferencije kupaca. Ovo pomaže finansijskim institucijama da svoje proizvode i usluge prilagode potrebama klijenata.

Osiguranje zajma: Neuronske mreže se mogu koristiti za automatizaciju i pojednostavljenje procesa preuzimanja kredita analizom informacija o podnosiocima zahteva i donošenjem preciznijih odluka o odobravanju kredita.

Predviđanje cene akcija: Neuronske mreže se mogu obučiti na istorijskim podacima o akcijama kako bi pokušale da predvide buduća kretanja cena akcija, što može biti korisno za strategije ulaganja i trgovanja.

Čet-botovi i virtuelni pomoćnici: Finansijske institucije koriste čet-botove i virtuelne asistente na neuronskim mrežama za pružanje personalizovane korisničke usluge i podrške, odgovaranje na pitanja i pomoć u zadacima.

Ključne prednosti korišćenja neuronskih mreža u bankarstvu uključuju poboljšanu tačnost, brzinu i skalabilnost u oblastima kao što su procena rizika, otkrivanje prevara i uvid u klijente. Ovo pomaže poveriocima da donesu bolje odluke i pruže bolju uslugu svojim klijentima.

U prethodnim godinama neuronske mreže su intezivno razmatrane kao alternative statističkim modelima.

Snaga i slabost neuronskih mreža može se sumarno prikazati kao (Abrahams et al., 2024):

-  Neuronske mreže lako modeliraju visokosložene, nelinearne odnose između inputa i outputa;

- One su oslobođene bilo kakvih pretpostavki o distribuciji;

-  Ovi modeli mogu biti brzo adaptirani na nove informacione inpute (u zavisnosti od algoritma treninga ili obuke);

-  Nema formalnih procedura koje bi odredile optimum i vrstu mreže za povezivanje slojeva i čvorova koji povezuju ulazne i izlazne promenljive;

-  Neuronske mreže su crne kutije pošto su vrlo teške za interpretaciju; i

-  Izračunavanje verovatnoće difolta je moguće samo do određenih granica uz znatan dodatni napor.

Neuronske mreže su delimično podesne u slučaju kada ne postoje očekivanja (zasnovana na iskustvu ili na teoretskim argumentima).

Analiza internog kreditnog rejtinga i procena efekata uvođenja Bazelskih standarda

Bazel standardi su delo Bazelskog skupa za bankarsku kontrolu, osnovani sa težištem da se prema unapred utrđenim pravilima proceni stepen rizika i to kreditnog, koji se nalazi u bankarskom kreditnom portfoliju odnosno njenoj aktivi. Ovi standardi ističu identifikaciju kreditnog portfolija određenih bankarskih klijenata, a zasnovani su isključivo na prihodima ostrarenim po osnovu prodaje (BCBS, 2006). Veliki broja bankarskih institucija je već prihvatio i primenio ovakavu vrstu identifikacije bankarskih klijenata, a isključivo za potrebe projektovanja kreditnog rizika. Utvrđivanje stepena rizika propisanog RW formulama Bazelskih standarda, čini završnu aktivnost u internoj proceni rejtinga i to kreditnog. Sličan vid procene i prognoze efekata primene Bazelskih standarda ističe se i u radu (Altman & Sabato, 2007), u kojem su prognozirani Bazelski standardi primenjeni za preduzeća u Americi.

Rezultati istraživanja su zaključili da se korišćenjem Bazel standarda i njegovih usavršenih i modernizovanih pravila smanjuju kapitalni zahtev prema kreditnim rizicima (Danielsson et al., 2021). Takođe bitno je istaknuti, da nema razlike u formulama Bazelskih pristupa I, II i III za deo preduzeća, a priliom utvrđivanja pondera rizika koji se primenjuju kod analize i vrednovanja kreditnog rizika.

Tabela 1. Bazel parametri i ponderi rizika za segment malih preduzeća, na osnovu uspostavljenog internog kreditnog rejtinga

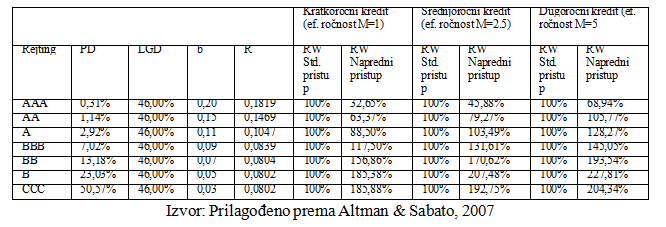
U Tabeli 1. prikazani su po definisanim rejting klasama sledeći pokazatelji rizika: PD (verovatnoća difolta), LGD (Gubitak pri difoltu Loss Given Default), b (faktor ročnog prilagođavanja koji odražava uticaj PD) i R (predstavlja korelaciju za izloženosti prema privrednim društvima), koji se smatraju bitnim faktorima u definisanim formulama (Hunt et al., 2020). Na osnovu ovih pokazatelja, za privredna društva manje veličine (gde ukupni godišnji prihod od prodaje iznosi 5 miliona EUR) formulisan je ponder rizika RW, koji odgovara savremenom konceptu Bazel-a. Pored toga, formulisan je i tradicionalan pristup i njemu određeni ponder rizika. Razlika u određivanju RW (ponder kreditnog rizika) postoji samo kod preduzeća velike veličine. Analizira pondera rizika po klasama intenog kreditnog rejtinga je prikazana i za različite ročnosti kredita. U propisanim formulama Bazela, ročnost je prikazana na osnovu pokazatelja efektivne ročnosti M, koji ima vrednost od 1 do 5. Za kredite u kratkom, srednjem i dugom roku prikazane su i određene referentne vrednosti ovog pokazatelja. Interesantno je zapaziti, da se stepen pondera rizika RW povećava, pri porastu ročnosti plasmana. Tako je na primer RWBBB, M (1) = 117,50% > RWBBB, M (5) = 145,05%, odnosno ponder rizika se povećava sa porastom ročnosti uzimajući PD vrednost za nepromenjenu veličinu. Takođe, interesantno je i zapaziti i situacije kada lošija rejting kategorija, sa većim procenjenim PD parametrom, ima manji RW. Ova situacija se događa kada vrednost PD dostigne tzv. tačku kontaminacije (eng. contamination point). Tako, na primer RWB > RWCCC, gde je RWB = 185,38%, a PDB = 23,03%, dok je RWCCC = 185,88%, a PDCCC = 50,57%.

Obrazloženo tumačenje za takvu situaciju stoji u oblazloženju da se za rejting klase koje dostignu tačku sistematizacije PD, ukupni kreditni gubitak većim delom formuliše iz očekivanog gubitka (EL), što dovodi do smanjenja neočekivanog gubitka (UL) koji neposredno zavisi od procenjenog RW tj. pondera rizika (Genest & Brie, 2013). Drugim rečima, nastupa promena u strukturi ukupnog gubitka i to prelivanjem neočekivanog u očekivani gubitak.

Tabela 2. Bazel parametri i ponderi rizika za segment srednjih preduzeća, na osnovu uspostavljenog internog kreditnog rejtinga 

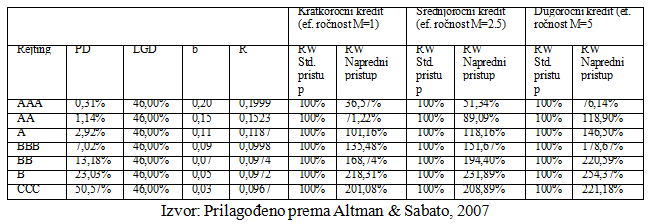
U Tabeli 2. Iskazani su prema unapred definisanim rejting klasama sledeći pokazatelji: PD, LGD, b i R parametri rizika, koji su definisani kao bitni fakotri propisanih formula, ali za privredna društva srednje veličine (ukupni godišnji prihod od prodaje jednak 25 miliona EUR). Formulisani su i iskazani, ponderi rizika RW, koji odgovaraju savremenom konceptu Bazel pristupa. Ako se izvrši upoređivanje podataka prikazanih u Tabelama 1. i 2., može se utvrditi da su ponderi rizika veći za privredna društva srednje veličine i to po svim rejting klasama i ročnostima. Objašnjenje za ovo može se naći u koloni R, koja definiše regulatorno određene korelacije, koje su zavisne od veličine privrednih društava. Stepen korelacije R, je obrnuto srazmeran stepenu diverzifikacije porftfolija (Crook, Edelman, & Thomas, 2007). Drugačije rečeno, difolt privrednog društva manje veličine u manjoj meri povlači difolte drugih privrednih društava, dok sa rastom njihove veličine ova međuzavisnost raste. Tabela 3. kao i Tabela 1. i 2. iskazuje parametre rizika i pondere rizika RW, za privredna društva velikih veličine (ukupni godišnji prihod od prodaje jednak 50 miliona EUR). Ponderi i parametri rizika, odgovaraju savremenom konceptu Bazel-a.

Tabela 3. Bazel parametri i ponderi rizika za segment velikih preduzeća, na osnovu uspostavljenog internog kreditnog rejtinga

Ako se izvrši upoređivanje podataka iskazanih u Tabelama 1., 2. i 3., može se utvrditi da su ponderi rizika, po svim rejting klasama i ročnostima, najveći kod privrednih društava velikih veličina. To utiče na pokazatelj RW, a zbog uvećanja koeficijenata korelacija. U Tabeli 3. pokazatelj RW ima najviše vrednosti po svim rejting kategorijama i ročnostima, za razliku od Tabele 1 i 2. Objašnjenje za opravdani prelazak na napredne koncepte za upravljanje rizikom, može se naći u zaključku sprovedene analize, da se umanjenje kapitalnih zahteva za kreditni rizik kod kredita u kratkom roku očekuje samo za prve tri najbolje rejting klase, što čini oko 52% ukupnog broja korisnika. Uzimajući u obzir da je u Tabeli 1, samo za ove pokazatelje naprednog pristupa RW niži za razliku od pokazatelja standardnog pristupa, moguće je samo za ove rejting klase postići uštedu tj. umanjenje kapitalnih zahteva. Kod kredita na srednjem i dugom roku u Tabeli 2. i 3. umanjenje kapitalnih zahteva za kreditni rizik se predviđa samo kod prve dve klase internog kreditnog rejtinga, što čini 30% ukupnog broja korisnika. U porođenju sa sprovedenim istraživanjem (Altman & Sabato, 2007), koji ističu da prognozirani efekti savremenog koncepta za merenje kreditnog rizika primenom standarda Bazel II dovode do smanjenja zahteva kapitalnih za kreditni rizik, ali na podacima američkih privrednih društava, u ovom radu je utvrđeno da bi efekat smanjenja zahteva kapitalnih postojao samo kod najboljih rejting klasa, u zavisnosti od ročnosti kreditnog plasmana, što čini 32% - 50% privrednih društava. S druge strane, kod svih drugih rejting klasa došlo bi do uvećanja zahteva kapitalnih za kreditni rizik u odnosu na tradicionalni koncept. Zato je na bankarskim institucijama u Srbiji da procene moguće efekte napredovanja i usavršavanja savremenog koncepta, a u pogledu korisnosti i mogućih troškova.

Zaključak

Metode, merenje i procena rizika unutar finansijskih institucija u poslednjoj deceniji su značajno unapređeni, što je uzrokovalo bolje predviđanje uspešnog poslovanja i smanjenje rizika, koji bi uzrokovali nemogućnost dužnika da svoje obaveze prema poveriocima ne mogu izvršavati blagovremeno ili ih uopšte ne mogu realizovati.

Nadalje, za neke klase izloženosti, Bazelski Komitet predlaže osnovnu metodologiju kojom finansijske institucije, kao ulaznu veličinu, uzimaju sopstvenu procenu rizika neplaćanja dužnika, a procene dodatnog faktora rizika su izvedene kroz primenu standardizovonih pravila supervizora.

Osnovna metodologija je dostupna za one finansijske institucije koje mogu da uvere supervizore da su sposobne da odgovore na specfične minimalne zahteve bankarskih sistema unutrašnjeg rejtinga, procesa upravljanja rizika i mogućnosti procene neophodnih komponenti rizika.

Aspekt pristupa zasnovan na internom rangiranju može biti realizovan na više načina. Prvo, tokom perioda i na nivou industrije, Bazelski Komitet očekuje da se sve više finansijskih institucija pomeraju od standardizovanog pristupa ka IRB pristupu i očekivanjima da će one to učiniti kada budu imale potrebne sisteme. Drugo, unutar IRB pristupa. od finansijskih institucija će se očekivati da se kreću od korišćenja osnovnog ka više naprednim metodologijama u skladu sa obogaćivanjem njihove prakse u upravljanju rizicima.

Pojedine finansijske intitucije su sposobne (ili će to postati) da sprovedu pogodnu i doslednu procenu dodatnih komponenti rizika, dok će drugima trebati više vremena da se prestruktuiraju na ovu vrstu procena. Ove dodatne komponente su gubici koji će nastati u slučaju neplaćanja dužnika, nivoa izloženosti dužnika u momentu neplaćanja, efekata garancija i rizika izloženosti kreditnih derivata. \

lstovremeno sa osnovnom metodologijom ustanovljene su i napredne metodologije koje omogućavaju da se koriste sopstvene unutrašnje procene komponenti rizika. Široko korišćenje takvih procena je jedan važan deo dinamičkog i risk-senzitivnog IRB pristupa na takav način da mogu da se prepoznaju i razlikuju one finansijske institucije koje su u mogućnosti da sprovedu dovoljno validnu i kvantifikovanu procenu rizika od onih koje to nisu u stanju.

Možemo zaključiti da validacija od strane finansijskih institucija uključuje dve ključne komponente-validaciju rejting sistema i procenu komponenti rizika i validaciju rejting procesa usmerenih na implementaciju rejtinga sistema. Validacija rejting sistema može nadalje biti razložena na dve komponente: evaluacija izrade rejting sistema ili izrade modela i procene komponenti rizika.

Finansijske institucije su u obavezi da poseduju sofisticirani sistem procene tačnosti i konzistentnosti rejting sistema, procesa, i interno pracene faktora rizika. Istorijski vremenski okviri za podatke koji se koriste u proceni stepena korelacije podataka treba da budu što je moguće duži i u idealnom slučaju da pokriju kompletan poslovni ciklus. Takođe ove institucije moraju do imaju na raspolaganju jasne stres testing procese koje koriste u proceni kapitalne adekvatnosti.

Testiranje mora da sadrži identifikaciju budućih promena ekonomskih uslova i mogućih događaja koji bi mogli nepovoljno uticati na procene difolta (neispunjenje obaveze dužnika) pa samim tim i na ukupni nivo kapitalne adekvatnosti. Testiranje na uslove stresa se mora sprovesti barem jednom u šest meseci. Rezultat testiranja periodično treba da se dostavi kroz izveštaj seniorskom menadžmentu banke.

Za procenu verovatnoće neplaćanja eksterni rejting podaci i interne procene verovatnoće neplaćanja, definicija difolt događaja i rezultirajuća definicija difolt rate (procena neplaćanja) moraju biti slične.

U ovom radu predstavljena je validacija internog kreditnog rejtinga, korišćenjem dostupnih analiza i tumačenja iz dostupne akademske literature. Rezultat sprovednog istraživanja, utvrdio je da je razvijeni interni kreditni rejting za sva privredna društva prošao sve preporuke validnosti i pravilnosti i da je u skladu sa stadardima Bazel koncepta. Takođe, on može da se koristi kao prvi korak kod interne procene potrebnog nivoa kapitala i pokrića mogućih očekivanih i neočekivanih gubitaka. Zato su u radu izračunati ponderi rizika (eng. risk weights - RW) koji se primenjuju kod vrednovanja rizičnosti plasmana na nivou bankarskog portfolija. Na kraju se može istaknuti da se sprovedena metodologija može primeniti na sve bankarske institucije koje posluju u Srbiji i Evropi.