Uvod

Istorijski smo svedoci mnogim krizama koje su se desile tokom 21-og veka. Najznačajnije su dve koje su pogodile celo svetsko tržište i to svetska ekonomska kriza 2008. godine i Covid19 kriza 2020. godine. Tema ovog rada se fokusira na kretanje četri indeksa u periodu od 2007. do 2022. godine, koji obuhvataju obe krize. Cilj je proceniti koja kriza je imala veći uticaj na pojedinačne indekse kao i na portfolio kreiran putem analize srednje varijanse. Takođe visina volatilnosti u vezi sa reakcijom na krize je izračunata putem VaR metode. Teorijski deo će biti fokusiran na objašnjenja analize srednje varijanse i VaR metoda kao centralnom delu rada.

Odnos rizika i prinosa je jedna od tema o kojima se najviše diskutuje na finansijskim tržištima, jer njegovo razumevanje omogućava investitorima da donose odluke. S toga, neki investitori su skloni riziku i ne žele da preuzmu dodatnu izloženost kako bi postigli veće prinose, dok sa druge strane postoje investitori koji su spremni da preuzmu veće rizike. Procena ove dve kategorije je stoga od najveće važnosti, bez obzira na vrstu investitora. U ovom radu rizik portfolija će biti izračunat primenom VaR metode, za koji je potrebno kreirati portfolio. Portfolio će se sastojati od četiri berzanska indeksa, čiji će ponderi biti dodeljeni na osnovu analize srednje varijanse (Takino & Ishinagi, 2022).

Što se tiče vremenskog okvira, globalna slika finansijskog sveta je obuhvaćena za period od aprila 2007. do januara 2022. godine. Ovaj vremenski okvir je izabran da pokrije period obe krize koje su se zadesile u 21-om veku. Tokom ovog perioda, fokus je na periodima u kojima je volatilnost pojedinačnih indeksa i portfolia bila veća, sa ciljem da se proceni koja kriza je imala veći uticaj kako na same indekse, tako i na kreirani portfolio. Takođe će rizik biti procenjen VaR metodom i kvantifikovan. Stoga, cilj rada možemo podeliti na dva problemska pitanja: 1. Uticaja kriza na izabrane indekse, sa nastojanjem da se proceni koja je imala snažniji uticaj, i 2. Kreiranje portfolia putem analize srednje varijanse i procena rizika putem VaR metode.

Teorijske osnove

Iako je glavna ideja da se proceni uticaj kriza na indekse, a potom portfolio, jaz u znanju će biti fokusiran na VaR metodu i analizu srednje varijanse. Uopšteno govoreći, VaR kao mera je usmerena isključivo na procenu rizikaNekoliko istraživača preporučuje upotrebu istorijskog VaR-a jer je ovo najjednostavniji metod. Nasuprot tome, postoje neki koji se ne slažu sa tim jer veruju da može da obmanjuje jer ne obuhvata neočekivane promene na tržištu. Još jedna poteškoća sa kojom se može zadesiti u suočavanju sa istorijskim VaR-om je pitanje koliko bi uzorak trebalo da bude veliki da bi obuhvatio sve distribucije povrata.

Druga vrsta VaR je delta-normal VaR, koji pretpostavlja normalnu distribuciju prinosa, što nije uvek slučaj i stoga je često nepraktično. Pored toga, EWMA metoda se može koristiti za izračunavanje VaR-a, sa prednošću što su noviji događaji ponderisani više. Tehnike koje rešavaju nedostatke ranijih metoda mogu biti računski zahtevne. Jedno od rešenja koja su preporučili mnogi autori je GARCH (Generilizovana autoregresivna uslovna heteroskedastičnost) metoda. GARCH metoda uključuje dodatni parametar u proračunu volatilnosti i stoga poboljšava tačnost VaR-a. Postoji dalje niz suprotstavljenih stavova o upotrebi VaR-a, a jedan od njih je upotreba mnogih metoda izračunavanja, što dovodi do različitih rezultata (Xiang & Zhang, 2022). U ovom radu autori će primenti računanje VaR metode putem metode normalne distribucija, kao metode koja je najzastupljenija u teoriji.

Pregled literature

VaR je mera rizika koja se uglavnom koristi za merenje rizične pozicije banke ili investicione kompanije. Rane 1990-te donele su neizvesnost na finansijsko tržište (Angelidis & Degiannakis, 2019), što je dovelo do razvoja različitih modela za procenu tržišnog rizika. Ovo je uticalo na stvaranje VaR-a 1995. od strane JP Morgana, koji je objavio dokument pod naslovom Risk Metrics (Morgan/Reuters, 1995). Dokument je predstavio šta je VaR i kako se može izračunati. Čak i pre objavljivanja dokumenta, VaR je predložen kao mere tržišnog rizika (Group of Thirty, 1993). Prema JP Morganu, VaR je mera gubitka sa datom verovatnoćom tokom vremenskog horizonta. Najvažniji parametar u njegovoj formuli je standardna devijacija kao mera disperzije. Standardna devijacija ili njena kvadratna verzija - vvarijansa mogu se izračunati na mnogo načina, npr. istorijska volatilnost, EWMA (Eksponecijalni ponderisani prosek), GARCH, itd. Sam VaR se može izračunati korišćenjem simulacionih modela kao što su istorijska simulacija ili Monte Karlo simulacija. VaR metode se mogu klasifikovati u tri kategorije: parametarske metode – delta-normalni pristup, neparametarske metode – istorijska simulacija i Monte Karlo metode (Nabella, Maski, & Wahyudi, 2020). Ovaj rad obuhvata delta-normalni pristup, koji podrazumeva normalnu distribuciju prinosa.

U literaturi postoje različiti pogledi. Na primer, istorijski simulacioni model je dao bolje rezultate predviđanja od drugih metoda koje se koriste ako je veličina uzorka dovoljno velika i ako je uključen viši nivo pouzdanosti (Craig, 2019). Metode simulacije su se pokazale kao bolje od parametarskih metoda kada je u pitanju procena VaR-a (Liu & Luger, 2022). Ipak, nedostatak je u tome što je istorijska volatilnost suviše jednostavan metod za izračunavanje volatilnosti koji koristi samo formulu standardne devijacije (Marra, 2017). U ovim osnovnim informacijama, razvijen je delta-normalni pristup koji uključuje matricu kovarijanse kao dodatni parametar za proračun. Spada u grupu parametarskih VaR metoda, sa glavnom pretpostavkom o normalno raspoređenim prinosima (Kulali, 2016).

Problem i cilj rada

Problem rada se fokusira na rešavanje pitanja koja kriza je imala snažniji uticaj na pojedinačne indekse kao i na celokupni kreirani portfolio. S obzirom da ekonomija kao celina ima cikluse, krize kao fenomen nisu nešto nepoznato. Ono što ostaje nepoznato jeste kada će se koja kriza desiti, i koji sektori će biti pogođeni. Direktno u vezi sa tim, ovaj rad nastoji da da odgovor kako su se koji indeksi ponašali tokom dve krize u 21-om veku. Analiza srednje varijanse se prvo vrši da bi se kreirao optimalni portfolio. Svrha kreiranja optimalnog portfolia je da se pronađe najbolji prinos putem kombinacije sredstava. Kada se kreira optimalni portfolio, primeniće se metoda delta-normal VaR. Osvrćući se na temu VaR, glavna namera je da se izračuna najveći mogući gubitak na portfoliju sa datom verovatnoćom u datom periodu (Buczynski & Chlebus, 2020).

Metodologija

Za potrebe analize uzeta su u obzir četiri indeksa. Svaki indeks predstavlja jednu klasu imovine, a indeksi pokrivaju i razvijena i nerazvijena tržišta, i slede:

1.       MSCI World Index: indeks akcija;

2.       Vanguard Total Bond Market Index Fund: indeks obveznica;

3.       S&P GSCI Index – indeks robe;

4.       Vanguard Real Estate Index Fund Investors – indeks nekretnina.

Za početak procesa optimizacije potrebno je prikupiti podatke za sva četiri indeksa od aprila 2007. do januara 2022. Godine. U ovom radu su dnevni podaci preuzeti sa veb sajta investing.com, sa namerom da se obuhvate sve promene. Shodno tome, podaci će biti uvezeni u Python, gde će se vršiti sve analize.

Analiza srednje varijanse

Ovo poglavlje se bavi temom analize srednje varijanse, fokusirajući se na proračun i njegovo fundamentalno razumevanje. Teorija srednje varijanse je deo moderne teorije portfelja koju je razvio Hari Markovic. Ispitivao je ulogu odnosa između rizika i prinosa i otkrio da su svi investitori neskloni riziku – preferiraju manji rizik za isti očekivani iznos prinos (Reilly & Brown, 2003). 

Svi investitori imaju za cilj da pronađu individualno optimalan portfolio. To znači kreiranje portfolija koji odražava njihove sopstvene preferencije u smislu investicionih očekivanja. Optimalni portfolio je portfolio koji ostvaruje najveći očekivani prinos za dati rizik, meren kao standardna devijacija (Hiller, 2022). Ova studija će koristiti portfolio kreiran od četiri različita indeksa akcija sa ciljem stvaranja optimalnog portfolia sa minimalnim rizikom. Ovaj portfolio će sadržati indekse koji odražavaju i razvijena i nerazvijena tržišta, kao i tržišta akcija, obveznica, nekretnina i roba. U tom smislu portfolio će odražavati celo tržište. Optimalni portfolio se može izračunati na osnovu cene na zatvaranju berze, očekivanog prinosa, standardne devijacije i korelacije. Očekivani prinos za portfolio može se izračunati na sledeći način (Markowitz, 1952):

 (1)

Gde je  očekivani prinos portfolia,  je ponderisanje svake klase sredstava u portfoliu i  su prinosi svih klasa sredstava. Prema tome, očekivani prinos portfelja je zbir ponderisanih prinosa svake klase sredstava uključenih u 
portfolio. S druge strane, varijansa portfolija nije jednostavno ponderisana standardna devijacija klasa aktive, jer njihova korelacija čini razliku u smislu procenjenog rizika. Diverzifikacijom je moguće postići manji rizik u portfoliju nego što ga ima sama akcija. Dakle, opšta formula za rizik portfolija može se izračunati na sledeći način (Hiller, 2022):

 2)

Gde je  portfolio varijansa,  je kovarijansa između svaka dva sredstva imovine. I-ti red i j-ta kolona je kovarijansa između promenljivih i i j. Kovarijansa između varijable i nje same je varijansa koja predstavlja dijagonalne ulaze u matrici (Hull, 2017).

 (3)

Dva ograničenja su data (Markowitz, 1952):

1.

2.

Prvo ograničenje je da zbir pondera svake klase imovine mora biti jednak 1, a drugo zabranjuje prodaju finansijskih instrumenata koji se ne poseduju.

Grafikon 1: Analiza srednje varijanse

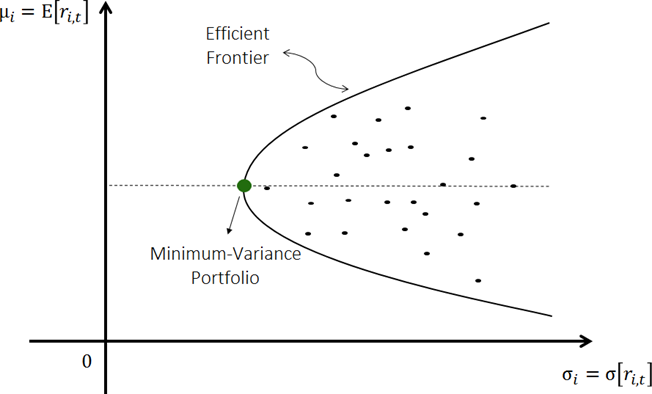
Izvor: (Goncalves, 2022)

Kada se izračunaju očekivani prinosi i rizik, sve njihove kombinacije mogu biti prikazane na grafikonu (Goncalves, 2022). Linija sa optimalnim portfeljima naziva se efikasna granica. X-osa prikazuje standardnu devijaciju, a Y-osa prikazuje povrat. Pomeranje ulevo od x-ose rezultira manjom varijansom. I suprotno, pomeranje udesno dovodi do veće varijanse. Pomeranje nagore do y-ose dovodi do većeg prinosa, pomeranje nadole znači niže prinose. Portfolio koji je najdalje levo na x-osi predstavlja portfolio sa minimalnom varijansom i prikazan je kao tačka. Portfoliji koji nisu na liniji ne daju bolje rezultate. Oni nude ili veći rizik za isti prinos ili manji prinos za isti rizik.

U ovom radu, kao što je već pomenuto, koriste se četiri berzanska indeksa, pa je formula za očekivani portfolio i varijansu sledeća:

 (4)

(5)

Jedna od prednosti koje je donela moderna teorija portfolija (MPT) jeste uticaj na trgovce da diversifikuju svoje portfelje umesto da se koncentrišu na jednu klasu sredstava. Iako je zasnovan na mnogim restriktivnim pretpostavkama, omogućio je procenu rizika portfelja i prinosa. Neke od glavnih pretpostavki su normalna raspodela prinosa i racionalno ponašanje investitora (Rice, 2017).

Value at Risk (VaR)

VaR je statistička mera koja se generalno koristi za analizu tržišnog rizika povezanog sa finansijskim sredstvima ili portfeljima (Mensink & Neves, 1999). Datira iz 1995. godine, kada je JP Morgan objavio RiskMetrics dokument, koji je objasnio VaR kao model. Pod tim imenom je definisan tek 1995. Godine. Nakon što ga je uveo JP Morgan, postao je široko korišćena mera izloženosti tržišnom riziku. On pruža jednostavnu i lako primenljivu kvantitativnu meru za procenu ukupnog tržišnog rizika kome je neko izložen. Takođe ga koriste mnogi menadžeri rizika za procenu potencijalnog gubitka portfelja tokom određenog vremenskog perioda i na određenom nivou poverenja.

Postoje dva ključna elementa za opisivanje VaR-a (Olsen, 2020):

1.    Vremenski horizont – što je veći horizont, veći je VaR. Kada se izračuna dnevni VaR, može se produžiti na više dana množenjem kvadratnog korena vremena. Ovo je slučaj kada su prinosi nezavisno i identično raspoređeni (iid) sa normalnom distribucijom (Jorion, 2007);

2.   Nivo poverenja – što je viši nivo poverenja, veći je VaR i više scenarija je pokriveno. Najčešće korišćene verovatnoće su one od 95% i 99%. Ovi elementi se mogu opisati u jednoj rečenici: "Mi smo X posto sigurni da nećemo izgubiti više ode V dolara u vremenskom periodu T" (Hull, 2015). VaR se stoga definiše kao iznos novca koji se može izgubiti tokom određenog vremenskog perioda na određenom nivou poverenja.

 (6)

Gde je  srednja vrednost,  je standardna devijacija portfolia,  je inverzna kumulativna normalna raspodela (Hull, 2017).

Može se reći da ako je VaR portfelja milion dnevno sa sigurnošću od 95%, postoji samo 5% šanse da će gubitak biti veći od milion. Nedostatak VaR-a je ovde izražen, jer ne govori ništa o iznosu gubitka ako dođe do ovih 5%. Iz tog razloga, VaR je često bio kritikovan i uvedena je dodatna mera, odnosno očekivani gubitak (ES) ili uslovni VaR (CVaR), koji meri prosek svih gubitaka koji su veći od VaR (Mendes, 2022). Upotreba CVaR-a umesto VaR-a ima mnogo prednosti, kao što je uključivanje gubitaka viših od VaR-a, što rešava jedan od problema povezanih sa VaR-om, ali praksa u finansijskoj industriji i dalje snažno favorizuje upotrebu VaR-a (Chipping, 2014). Drugo ograničenje VaR-a je to što daje različite rezultate u zavisnosti od korišćene metode (Bedi, Shankar, Agnihotri, & Kalra, 2018). Daljnji nedostatak o kome se raspravlja je to što VaR nema sub-aditivnost, što znači da VaR portfelja može biti veći od zbira pojedinačnih VaR-ova (Meissner, Bhaduri, Linsky, & Yuan, 2021) što uzrokuje probleme agregacije (Chen, Sit, & Wong, 2019). Rešenja za većinu nedostataka VaR-a nalaze se u CVaR-u, kao što su subaditivnost i konveksnost (Francq & Zakoian, 2019).

Rezultati rada sa diskusijama

Ovo poglavlje opisuje rezultate rada. Nakon unosa biblioteka i skupa podataka u programski jezik Python, prinosi za svaki indeks se izračunavaju.

Dijagram 1: Prinosi sva četri indeksa

Izvor: Autor na osnovu podataka sa Platforme investing.com

Kada se pogleda prezentacija prinosa sva četiri indeksa na sledećem dijagramu, može se zaključiti da je:

1.      The Vanguard Bond index najmanje volatilan, jer njegove crvene linije nisu vidljive na grafikonu, tj. najniža volatilnost;

2.      S&P Commodity indeks nije toliko izražen u poređenju sa drugim indeksima;

3.      The MSCI World Index pokazuje veće devijacije i odstupanja, kao i Vanguard Real Estate indeks u poređenju sa gore navedenim indeksima, i pokazuje najveću devijaciju tokom 2008. godine, dok MSCI World indeks pokazuje najveća odstupanja tokom 2020. godine.

Sa ovim rezultatom, sada je moguće pronaći odgovarajuće ponderisanje koristeći teoriju portfolija. U ovom trenutku portfolio se može izračunati sa minimalnom volatilnošću generisanjem nasumičnih portfelja i pronalaženjem najniže standardne devijacije za date pondere. Na osnovu prethodnog grafikona, očekuje se, između ostalog, da će Vanguard Bond index biti relativno zastupljeniji i da će Vanguard Real Estate i S&P Commodity indeks, kao najpromenljiviji indeksi, dobiti manje pondere. Pošto je investitor u ovom slučaju nije sklon riziku, bira se alternativa koja nudi minimalnu volatilnost. Računarska kalkulacija korišćenjem analize srednje varijanse predlaže sledeće pondere:

1.      Vanguard Bond Index - 91.01%;

2.      S&P Commodity Index - 1.94%;

3.      Vanguard Real Estate Index - 5.90%;

4.      MSCI World Index - 1.15%.

U poređenju sa očekivanjima, svaka tačka je potvrđena, odnosno veći udeo Vanguard Bond indeksa i niži udeo Vanguard Real Estate i S&P Commodity indeksa. Dijagram 2 prikazuje sve moguće kombinacije portfelja. Investitor može da bira između svih tačaka na grafikonu, pri čemu je maksimalni Šarp racijo prikazan crvenom tačkom, a minimalni promenljivi portfolio ljubičastom tačkom. U ovom slučaju, investitor nije sklon riziku, tako da je izabrana ljubičasta tačka koja je najdalje levo. Ova tačka nudi minimalnu volatilnost, za dati prinos.

Dijagram 2: Simulirana optimizacija portfelja zasnovana na Efficient Frontier-u

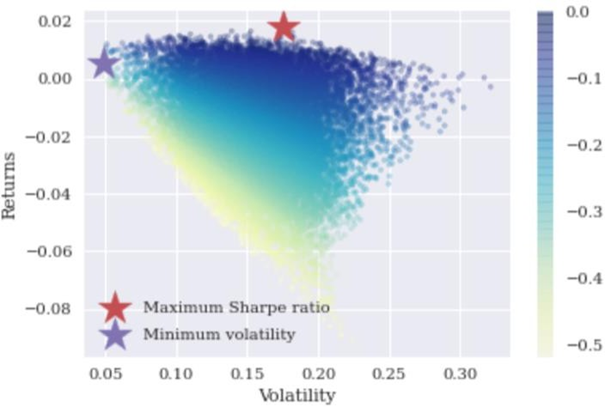
Izvor: Autor na osnovu podataka sa Platforme investing.com

Nakon dodele pondera, prinos portfelja se može prikazati grafički za dati period na dijagramu 3. Kao što se vidi na posebno iscrtanim indeksima, tako i ovde najveće odstupanje se može uočiti na kraju 2008. i 2020. godine Prinosi se kreću od -3 do +4 % u 2008. godini, dok u 2020. godini variraju od -6 do +4%, što potvrđuje da je kriza 2020. godine imala snažniji uticaj na sve klase imovine, čak i na kreirani portfolio za investitore koji nisu skloni riziku.

Dijagram 3: Ponderisani prinosi portfolia

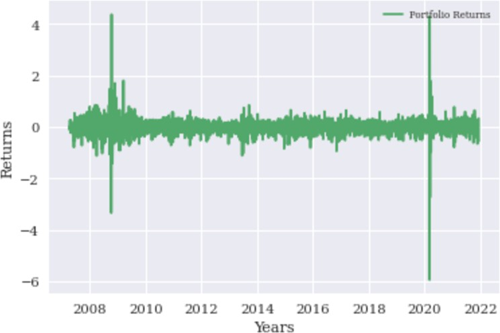
Izvor: Autor na osnovu podataka sa Platforme investing.com

Dijagram 4: Histogram portfolio prinosa

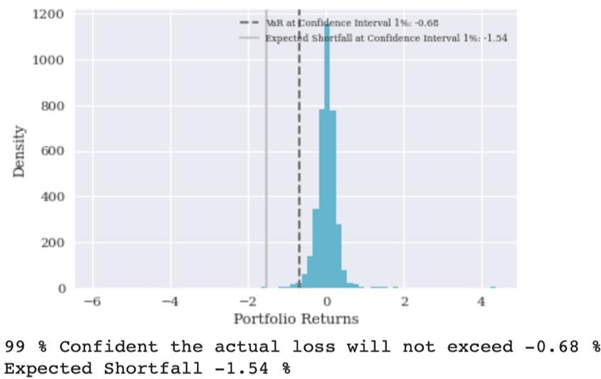
Izvor: Autor na osnovu podataka sa Platforme investing.com

Dijagram 4 prikazuje distribuciju svih prinosa portfelja za period od aprila 2007. do januara 2022. godine koristeći dve mere: svetlosiva linija pokazuje očekivani gubitak(ES), a tamna tačkasta linija VaR.

VaR se ovde izračunava kao jedan procentil sortiranih negativnih prinosa, i može se biti 99% sigurno da stvarni gubitak portfelja neće preći 0,68% vrednosti portfelja u jednom danu, dok očekivani gubitak je uvek veći i iznosi 1,54%, računato kao prosek najvećih gubitaka.

Na osnovu rezultata deskriptivne statistike može se zaključiti da prinosi nisu normalno raspoređeni. Standardna devijacija je manja, asimetrija veća i kurtozis mnogo veći nego kod normalno raspoređenih prinosa. Iz rezultata može se implicirati da su prinosi blago negativno iskrivljeni, a da je kurtozis pozitivan - leptokurtik. Ovde se može prepoznati rizik od ekscesa, što znači da u nekim slučajevima dobijamo preterane prinose, bilo pozitivne ili negativne, u statistikama poznatim kao ekstremni repovi.

Zaključak

U ovom radu obrađene su različite teme vezane za programiranje, statistiku i finansijsko modeliranje sa glavnom idejom sagledavanja finansijskih kriza u 21- om veku. Nakon čitanja različite dostupne literature, jaz je identifikovan, čijom definicijom počinje rad. Zatim se detaljno opisuje metodologija istraživanja. Formule, grafikoni, parametri su definisani i predstavljeni, kao i izvori koji se koriste, tako da čitalac može da ih koristi ako mu je neki deo teško razumljiv. Rezultati proračuna i analize su detaljno opisani.

Glavni zaključak ovog rada jeste da je kriza u 2020. godini imala snažniji uticaj na sve indekse, i dovela do većih volatilnosti u prihodima nego što je kriza tokom 2008. godine. Dalje, portfolio kreiran putem analize srednjih vrednosti za investitore koji nisu skloni riziku je potvrdio ove rezultate, pokazujući najveću volatilnosti u prihodima celog portfolia u 2020. godini. Takođe, VaR je izračunat sa ciljem da se proceni i kvantifikuje rizik. Tako rezultat VaR-a sa 99% sigurnošću je kvantifikovao da gubitak portfelja neće preći 0,68% vrednosti portfelja u jednom danu. Očekivani gubitak (ES) je uvek veći i iznosi 1,54%, računato kao prosek najvećih gubitaka.