Uvod

Opstanak države podrazumeva postojanje zdravog privrednog i poslovnog okruženja. Osnovne jedinice koje obezbeđuju funkcionisanje privrede su preduzeća koja u njoj posluju. Preduzeće, da bi opstalo na tržištu, pod uslovom da ne postoji monopolska pozicija nekog privrednog subjekta, mora da bude bude konkurentno. Svoju konkurentnost, preduzeće čuva napretkom i razvojem. Da bi ovo postiglo, neophodna su mu novčana sredstva za finansiranje rasta i razvoja, što postiže pravilnim odabirom i ulaganjem u investicione projekte.

Funkcionisanje javnog sektora uslovljeno je stalnim zadovoljenjem opštih i zajedničkih potreba društva. Usled konstantnog rasta sve složenijih javnih rashoda javlja se potreba za njihovim bilansnim nadomeštavanjem na strani javnih prihoda. Budžet kao jedan od instrumenata za finansiranje javnih rashoda je limitiran, najčešće na godišnjem nivou. Finansiranje investicionih projekata zahteva poseban tretman u domenu, kako planiranja tako i izvršenja budžeta, s tim u vezi javlja se potreba za finansijskom ocenom investicije za potrebe programskog budžetiranja.

 U domenu korišćenja metoda ocene investicija fokusiraćemo se na dinamičke metode: neto sadašnja vrednosti i interna stopa prinosa, kao i na statičke metode, ekonomičnost i rok povraćaja sredstava. Hipoteza od koje se u radu polazi, je da pravilan izbor ocene investicionog projekta bitno utiče na sve dalje postupke prilikom investiranja u dalji rast preduzeća kao i na uspeh ulaganja u investicioni projekat za koji se preduzeće opredelilo.

Metode ocene investicionih projekata

Ulaganjem u projekat, investitor očekuje da ostvari stopu prinosa na uloženi kapital. Angažovanjem sredstava u neku od opcija on veže svoja sredstva na određeni vremenski period. Ako bi ista sredstva uložio u banku dobiće kamatu na depozit po unapred obračunatoj kamatnoj stopi. Osnovni cilj kod ulaganja je da stopa prinosa bude veća od ove kamatne stope. Menadžeri koji koriste sredstva koja su investitori uložili moraju da imaju u vidu da ta sredstva više vrede sada nego što će u budućem periodu. Menadžeri moraju da imaju u vidu vremensku vrednost novca.(Puška, Beganović & Šadić, 2018; Damnjanović, 2017)

Kamata je cena korišćenja tuđeg kapitala. Iznos kamate je funkcija tri varijable: prvobitno pozajmljenog iznosa (glavnice), kamate za pozajmljeni vremenski period, kao i broja vremenskih perioda (broja godina) na koji se pozajmljuje glavnica.

 Formula za obračun ovako jednostavno definisane kamate može se napisati kao (Petrović, Đedović, & Petrović, 2013):

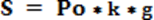
gde je:

S – jednostavno definisana kamata u novčanim jedinicama,

P0 – glavnica ili inicijalno pozajmljeni iznos u vremenskom periodu 0, k – kamata za vremenski period,

g – broj vremenskih perioda, odnosno broj godina.

Ovo je formula za obračunavanje jednostavne kamate. Ovo je kamata koja se plaća samo na prvobitan iznos. Odnosno, za bilo koju jednostavnu kamatu, buduća vrednost (FV) na kraju g – tog perioda bi se mogla napisati (Popović, Stanković, & Veselinović, 2013):

FVg = Po + S = Po + Po * k * g

U slučaju da vrednost glavnice nije poznata, prethodni izraz može se zapisati kao:

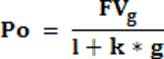
Vremenska vrednost novca ne može se izraziti kroz jednostavnu kamatu. Neophodno je izračunati složenu kamatu (Compound interest). U ovom slučaju kamata se obračunava na kamatu i na glavnicu (kamata na kamatu ili složeno ukamaćivanje). To znači da se kamata koja je plaćena periodično dodaje na glavnicu. Što se može predstaviti pomoću sledeće formule(Çağlar, Gürel, 2018):

 FVg = Po * (1+k) ^g

odnosno FVg=P0 * (FVKFk,g)

 gde je FVKFk,g – buduća vrednost kamatnog faktora, pri kamatnoj stopi k%, i vremenskom periodu od g godina, i može se iskazati (1+k) ^g.

Finansijska tablica olakšava praćenje postupka ukamaćivanja, budući da daje već izračunate vrednosti kamatnog faktora za kamatnu stopu k, i vremenski period od g godina. Može se reći da je ukamaćivanje proces definisanja buduće vrednosti iznosa s kojim raspolažemo u ovom momentu. Odgovor na pitanje koliko se novca, za koji se očekuje da će se obezbediti u nekom vremenskom periodu od g godina, i pri kamatnoj stopi od k%, može dobiti sada, je tehnika diskontovanja. (Keers, Van Fenema, 2018)

 Diskontovanjem se buduća vrednost svodi na sadašnju. Proces diskontovanja se realizuje diskontnom stopom (Discount rate). (Drljača-Kanazir, 2015) Diskontnom stopom se budući tokovi novca svode na sadašnju vrednost. Ova stopa je i merilo oportunitetnog troška. Oportunitetni trošak je vrednost koja je mogla biti ostvarena da su resursi bili uloženi u neki drugi projekat. Oportunitetna vrednost je, dakle, vrednost koja je propuštena jer kapital nije uložen u najbolju alternativu. (Popović, Stanujkić, & Stojanović, 2012; Volden, 2018)

Određivanje sadašnje vrednosti (ili diskontovanje - Discounting) je u osnovi obrnut postupak od složenog ukamaćivanja. Jednačina za izračunavanje sadašnje vrednosti (PV) se može napisati kao(Petrović, Đedović, & Petrović, 2012; Puška, 2011):

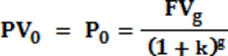, odnosno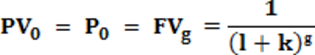

 Može se uočiti da je izraz 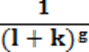 recipročna vrednost kamatnog faktora za buduću vrednost kamate od k%, i za period od g godina, odnosno PVKFkg. Ta recipročna vrednost ima svoje ime - diskontni kamatni faktor za k% za vremenski period od g godina, odnosno PV0 = FVg * (PVIFk,g), ova vrednost je tkđ. izračunata u finansijskim tablicama.

 Menadžment zadužen za rad na oceni investicionih projekata ima na raspolaganju nekoliko metoda. U zavisnosti od konkretne situacije moguće je koristiti samo jednu ili kombinaciju od nekoliko. Da bi se izbegle greške i umanjio efekat loših strana metoda najbolje je kombinovati metode.

Primena metoda ocene investicija

Način izračunavanja perioda povraćaja može se pokazati primerom na dva projekta sa različitim novčanim tokovima u celom periodu efektuiranja. Za primer smo uzeli potencijalno ulaganje VU „Dedinja“ u restoran u hotelu „Breza“ u Vrnjačkoj banji, u daljem tekstu projekat A i restoran u kantini u centru Beograda – objekat na uglu Resavske i Nemanjine ulice, u daljem tekstu projekat B. Oba objekta usluge pružaju pripadnicima GŠ VS i MO RS, kao i spoljnim korisnicima. Projekti imaju investicione troškove od 3.000.000,00 RSD i ekonomski vek trajanja od 5 godina. Novčani tokovi su projektovani na osnovu predhodnih godina poslovanja, tako da ukupni prihodi budu isti, radi boljeg poređenja rezultata primene metoda ocene investicionih projekata. (Milanović, Milanović, & Misita, 2010) U tabeli 1 se mogu videti investicioni troškovi i novčani tokovi projekata.

Tabela 1: Investicioni troškovi i novčani tokovi projekata A i B

Izvor: Delo autora

 Za izračunavanje perioda povraćaja za projekata pogledaćemo kolonu sa kumulativnim novčanim tokom projekta. Period povraćaja za projekat A biće 3 godine i 4 dana, dok će za projekat B biti potrebno 3 godine i 18 dana. Na osnovu ovih podataka, rentabilnije je uložiti u projekat A. U dalje tekstu pokazaćemo kako se ponašaju novčani tokoviprimenom metoda ocene investicionih projekata i pokušaćemo da dokažemo da je ulaganje u restoran u Resavskoj ulici rentabilnije.

 Za razliku od izvornog perioda povraćaja, kod diskontovanog se akumuliraju diskontovani novčani tokovi umesto originalnih neto novčanih tokova. Prilikom izračunavanja, prvo se diskontuju neto novčani tokovi uz primenu diskontne stope. Potom se vrši akumuliranje ovako diskontovanih neto novčanih tokova. Godina u kojoj zbir diskontovanih neto novčanih tokova dostigne vrednost troškova investiranje predstavalja diskontovani period povraćaja.

Izračunavanje sadašnje vrednosti novčanih tokova projekta A i B, uz diskontnu stopu od 10, za preduzeće koje ima nameru da investira u isplativiji projekat prikazano je u tabeli 2.

Tabela 2: Sadašnja vrednost novčanih tokova i diskontovani period povraćaja

Izvor: Delo autora

 Upoređivanjem perioda povraćaja, osnovnog i diskontovanog na primeru projekata A i B, dolazimo do zaključka da se primenom diskontovanih novčanih tokova period povraćaja produžuje. Menadžment bi oba projekta odbacio ako bi prag efikasnosti bio tri godine, a kao metod za ocenu diskontna stopa povraćaja.(Petrović, Đedović, & Petrović, 2013)

 Postupak izračunavanja neto sadašnje vrednosti možemo ilustrovati na predhodno korišćenim projektima A i B (tabela 3):

 Tabela 3: Proračun neto sadašnje vrednosti projekata A i B

Izvor: Delo autora

 U tabeli 3 se može videti da oba projekta, pri diskontnoj stopi 10, imaju pozitivnu neto sadašnju vrednost. Preduzeće B ima veću neto sadašnju vrednost. Kriterijum za prihvatanje projekta po metodu neto sadašnje vrednosti je kao što smo već naveli:

 Kada treba da se odlučimo za neki projekat na osnovu neto sadašnje vrednosti opredelićemo se za onaj koji ima najvišu neto sadašnju vrednost. U našem slučaju ulagaćemo u projekat B.

 Viša diskontna stopa smanjuje neto sadašnju vrednost, dok niža utiče na njen rast. Ako bi smo u našem primeru diskontnu stopu podigli na 15 dobili bi smo sledeće rezultate (tabela 4). Oba projekta su i dalje rentabilan pošto je neto sadašnja vrednost veća od nule. Uticaj diskontnih stopa na visinu neto sadašnje vrednosti može se prikazati kao u tabeli 5.

Tabela 4: Neto sadašnja vrednost novčanih tokova projekata A i B uz diskontnu stopu od 15%

Izvor: Delo autora

Bez diskontovanja projekat A je rentabilniji, međutim, uvođenjem diskontovanja projekat B je uvek rentabilniji od projekta A. Razlog tome je različita dinamika priliva ukupno jednakih novčanih tokova kroz jednako vreme efektuiranja.

 Tabela 5: Neto sadašnje vrednosti projekata A i B za različite diskontne stope

Izvor: Delo autora

 Rekli smo da se za izračunavanje neto sadašnje vrednosti koristi trošak kapitala preduzeća. Ovaj kriterijum omogućava merenje doprinosa svih novčanih tokova projekta u periodu realizacije sadašnje vrednosti. Upravo ovaj trošak kapitala, putem diskontne stope, direktno utiče na neto sadašnju vrednost. Kako se za diskontnu stopu uzima vladajuća kamatna stopa, ona se uglavnom malo uveća, sa ciljem da se približi realnoj situaciji, gde dolazi do promene kamatne stope.(Ribeiro, Domingues, 2018) Kada je period efektuiranja dugačak, veoma je teško izabrati realnu kamatnu stopu. Uglavnom se kao poboljšanje preporučuje korišćenje analize uticaja različitih vrednosti diskontnih stopa na neto sadašnju vrednost.

Prilikom izračunavanja interne stope prinosa odabere se diskontan stopa za koju se smatra da je najbliža internoj stopi prinosa. Ukoliko ona to nije, postupak izračunavanja se nastavlja sve dok se ne dođe do nulte vrednosti neto sadašnje vrednosti. Primer izračunavanja možemo videti u tabeli 6 i 7na primeru projekta A i B.

Tabela 6: Postupak izračunavanja interne stope prinosa projekta A

Izvor: Delo autora

 Tabela 7: Postupak izračunavanja interne stope prinosa projekta B 

Izvor: Delo autora

 Da bismo došli do prave diskontne stope primenićemo postupak linearne interpolacije. Prilikom izračunavanja će se koristiti dve diskontne stope, jedna pri kojoj je neto sadašnja vrednost pozitivna, i druga pri kojoj je negativna.

U našem slučaju interna stopa prinosa za projekat A bi iznosila 34.96, do bi za projekat B ona bila 37.77.

 Neto sadašnja vrednost nas upućuje na veličinu promene vrednosti običnih akcija u odnosu na njihovu sadašnju vrednost. Interna stopa(Giglio, Friar, Crittenden, 2018) će, za razliku od neto sadašnje vrednosti, samo odrediti smer promene vrednosti, ali neće pokazati veličinu te promene. Ove dve metode povezuje trošak kapitala, koji značajno utiče na obe.

 Izračunavanje neto sadašnje vrednosti ne znači da nema potrebe da utvrdimo vrednost interne stope prinosa, kako bi poboljšali donete odluke. Detaljnija analiza će menadžmentu olakšati odluku u vezi izbora pravog projekta. Postupak izračunavanja indeksa profitabilnosti je isti kao i kod neto sadašnje vrednosti sve do sumiranja sadašnjih vrednosti novčanih tokova. Diskontovani novčani tokovi se na kraju dele s troškovima investicije. Postupak izračunavanja možemo predstaviti na primerima projekata A i B, sa diskontnom stopom 10 (tabela 8).

 Tabela 8: Indeks profitabilnosti 

Izvor: Delo autora

 Pošto se od indeksa profitabilnosti očekuje da ima što veću vrednost, projekat B je prihvatljiviji od projekta A. Primena neke od metoda zavisi i do samog projekta. S tim u vezi možemo zaključiti da je potrebno pored toga obratiti pažnju i na odnos projekata koje upoređujemo, potreba racionalizacije kapitala, visinu projektnih rizika i nivo troškova investiranja.

Zaključak

Glavni preokret u ljudskom razvoju predstavljala je pojava robno – novčane razmene, a potom i privrede, gde se višak proizvoda prodavao, odnosno stvarao pa prodavao sa ciljem stvaranja dobiti. Danas imamo pojavu različitih oblika trgovine, gde ni roba, ni novac nisu fizički prisutni. Ovo je definitivni pokazatelj napretka, cilj je ubrzavanje obrta robe i otpočinjanje novog ciklusa proizvodnje. Osnovna gradivna jedinica svake privrede je preduzeće. Stanje privrede zavisi od snage i mogućnosti preduzeća da se razvijaju i šire svoju proizvodnju Preduzeće se razvija zahvaljujući ulaganjima u investicione projekte, koji savremenim tehnologijama smanjuju troškove poslovanja, u procesu proizvodnje postojećih proizvoda, odnosno uvode novi proizvod. Na ovaj način obezbeđuju preduzeću da uspešnije posluje i bude konkurentnije na tržištu.