Mathematical Model for Determining the Price of Shares – With the Impact of Inflation
Abstract
For investment decisions is developed larger number of mathematical models. The model has two parts, the function of the criteria and system limitations. Function criterion represents a special way, the aim sought to be achieved by solving problems.
Since it expresses the quality of the individual solutions, it serves as a measure of comparison in choosing the best solution. The system consists of a quantitative restriction limiting factors expressed in the functioning of the economic system.
These restrictions are a result of limited resources or other characteristics of the system. The system limits determine the scope of permissible solutions rešavanog problems. Mathematical models represent an important and useful tool in determining the price of shares in the context of investment decisions.
Article
Uvod
Osnovni pokazatelј na osnovu kojeg se određuje i meri opravdanost ulaganja u akcije predstavlja tržišna cena akcija jer ukazuje na kvalitet i uspešnost poslovanja preduzeća. Na opravdanost ulaganja utiče veći broj faktora među kojima se kao najvažniji mogu izdvojiti: celokupna situacija u ekonomiji zemlјe (pokazatelji: inflacija, kretanje deviznog kursa, kreditini rejting zemlјe...), pokazatelji poslovanja preduzeća koje je izdalo akcije (profitabilnost, efikasnost, način finansiranja, stepen zaduženosti, likvidnost isl.), kao politička stabilnost.
Kada je procenjena ili realna vrednost akcije iznad njene tržišne cene, reč je o njenoj potcenjenosti i tada racionalan investitor se opredeljuje za kupovinu akcija na berzi. U suprotnom, ukoliko je tržišna cena iznad realne vrednosti akcija, reč je o precenjenoj vrednosti, što podstiče investitore da se odlučuju na prodaju akcija.
Sve faktori koji utiču na cenu akcija možemo podeliti na eksterne i interne faktore, pri čemu eksterni faktori određuju makroekonomski ambijent u kojem preduzeće posluje i tu spadaju: ekonomska aktivnost – BDP, inflacija, devizni kurs, platni bilans zemlјe, spolјni dug, stanje u industrijskoj grani, odlike tržišta na kome kompanija egzistira, politički faktori itd. Interni faktori su određeni poslovnim uspesima preduzeća i oni se dobijaju analizom finansijskih izveštaja, kao i drugih informacija koje utiču na poslovanje preduzeća. Osnovni interni faktori su: profitabilnost kompanije, struktura izvora finansiranja, nivo tekuće likvidnosti, reputacija i kvalitet menadžmenta, vlasnička struktura, itd.
Osnovno pitanje za svakog investitora je utvrditi način kako predvideti buduće kretanje cena akcija, jer je tržišna vrednost akcije rezultat odnosa ponude i tražnje na tržištu kapitala. Imajući u vidu da delovanje ponude i tražnje i formiranje tržišnih cena akcija u krajnjem svodi tržišnu vrednost na unutrašnju vrednost akcija, koja se naziva i realnom vrednošću akcija od izuzetnog je značaja da ulokiko je tržišna cena akcija niža od njene realne vrednosti, tada će investitor odlučiti da kupi te akcije. Inače, realna vrednost se izračunava tzv. diskontovanjem, gde je cena akcija izražena kroz odnos dividende i stope kapitalizacije, a stopa kapitalizacije predstavlјa diskontnu stopu.
Inkorporiranje faktora rizika u cenu akcija
Kupovinom akcija njen posednik dobija pravo na korišćenje dividende kao i druga prava koja mu ona donosi. Svaki ulagač u tom smislu pred sobom ima alternativu u pogledu plasiranja kapitala koja se odnosi na izbor između dva osnovna rešenja. Prvo rešenje je da novac uloži u banku i da dobije kamatu koju mu daje banka na odgovarajuću vrstu depozita. Stepen rizika koji se u tom slučaju javlјa je relativno mali a mogućnost povlačenja depozita u stabilnim uslovima je neograničena. Banka je, dakle, uvek zahvalan partner za svakog potencijalnog posrednika kapitala. Drugo rešenje treba da ponudi neko ko bi mogao da bude atraktivniji partner od banke i ko bi mogao da ispuni bar dva uslova, a to su: veća zarada nego u banci i da se pri tom minimizuje rizik od takvog ulaganja. Ukoliko je taj partner akcionarsko preduzeće, to znači da ponudi dividendu koja je veća od bančine kamate. U protivnom svako ulaganje gubi smisao jer niko nije spreman da svoj kapital plasira u preduzeće čija je profitna stopa niža od bankarske kamatne stope. Takvo preduzeće je onaj privredni subjekat koji po logici zakona vrednosti silazi sa scene, koji je dakle ozbilјan kandidat za likvidaciju, a to znači i za totalni gubitak kapitala koji je uložen u njega.
Upravo zbog toga ovakve mogućnosti u nekim zemlјama nisu predviđene kao zakonsko rešenje, a u nekim su čak i zabranjene. Pošto se pred vlasnikom finansijskog kapitala nalazi mnoštvo mogućih kupavca hartija od vrednosti, onda bi bilo logično da se prodavac kapitala opredeli da svoje preferencije u nabavci hartija od vrednosti poveri onom prodavcu koji mu nudi najveću profitnu stopu i najmanji rizik. Prema tome, prodavac finansijskog kapitala će u ostalim jednakim okolnostima uvek radije kupiti akcije koje mu donose veću stopu dividende. U tom smislu on će rezonovati približno na ovakav način: ako nabavi akcije preduzeća koje daje dividendu za jedan procenat veću, to znači da će njegov dobitak biti za toliko veći. Tako bi bilo da te činjenice nije svestan i prodavac akcija. On je takođe u položaju da može da koristi različite izvore finansiranja uklјučiv i kredit, odnosno druge oblike hartija od vrednosti. Prema tome, svaki izdavalac akcija, svestan činjenice da je sposoban da daji više, podiže cenu svojih akcija. Upravo zbog toga cena ovih hartija od vrednosti neće biti onolika koliko bi se dobilo da se kapital prodaje banci. Ako on nudi dva puta veću dividendu, to znači da je spreman da svoje akcije proda, ali samo pod uslovom da kupac dobije dva puta veću količinu kapitala. Teza da je tržišna vrednost akcija proporcionalna odnosu između dividende i kamatne stope se u globalu potvrđuje u životnoj realnosti.
U sledećem primeru prikazaće se navedeno. Ukoliko preduzeće nudi licu akciju od 100 dinara i za nju plaća dividendu od 20% na kraju godine, lice će dobiti 20 dinara zarade. Ako za tu zaradu treba da plati dvostruko više to znači da će biti u položaju da blokira svoj kapital u vrednosti od 200 dinara sa 10% zarade. Ukoliko bih tu svotu novca stavilo na rasplaganje banci, opet bih dobilo 20 dinara kamate uz kamatnu stopu od 10%. Dakle, u obe situacije je na istom ali po jednom daleko jednostavnijem postupku i sa manje rizika.
![]()
![]() Zaklјučak je da pod dejstvom datih uslova lice nije spremno da bude akcionar. Da bi to bilo, uslov je da zarada bude viša od kamate. Upravo iz tih razloga ne postoji proporcija po kojoj se cena akcija po obrascu(Salvatore,1989):
Zaklјučak je da pod dejstvom datih uslova lice nije spremno da bude akcionar. Da bi to bilo, uslov je da zarada bude viša od kamate. Upravo iz tih razloga ne postoji proporcija po kojoj se cena akcija po obrascu(Salvatore,1989):

Pošto se pravno ili lice koje plasira svoj kapital u ovim okolnostima nalazi u neutralnoj poziciji, ono neće biti zainteresovano za takav aranžman, te za njega ova jednačina nema nikakvog praktičnog smisla.
Za njega će od značaja biti da prethodna jednačina ima sledeći oblik:
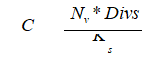
Dalјe u jednačini treba izvršiti inkorporiranje faktora rizika u cenu akcija. Već sama činjenica da su određeni poslovi rizičniji od drugih nameće obavezu da se ulagači kapitala obezbede od tako povećanih rizika. U konkretnom slučaju to bi značilo da je nekorektna jednačina po kojoj se utvrđuje cena akcija i koja glasi:
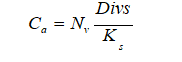
Ovo iz razloga što ona podrazumeva da je kupac akcije pod ovim uslovima suočen sa problemom povećanog rizika koji nije ulkalkulisan. Iz tih razloga on se nikada neće opredeliti da prihvati kupovinu akcije pod takvim uslovima. Za njega će ovi uslovi biti korektni ako se cena akcija redukuje na taj način što će se prethodna jednačina iskazati u sledećem obliku(Kulić, 2010):
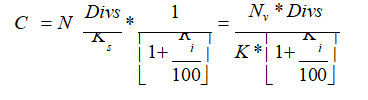
Pri čemu je
Ri = stopa rizika od ulaganja
Ako je u prethodnom primeru stopa rizika 6% to znači da će cena jedne akcije ovog preduzeća imati vrednost od:
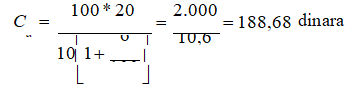
Na ovaj način je uspostavlјena jednakost koja dovodi do indiferentne pozicije, odnosno do toga da je ovo ulaganje nestimulativno za ulagača. Prema tome, obrazac za utvrđivanje cene akcije ovog preduzeća glasio bi:
Ca 188,68 dinara
U ovom kontekstu treba odrediti vrednost koeficijenta rizika. Odnosno doći do odgovora kako se dolazi do stope rizika od 6%. U teoriji se ovo pitanje uzima kao problem koji ima statističku podlogu i bazira se na visini standardne devijacije. Postupak utvrđivanja koeficijenta rizika u tom smislu svodi se na utvrđivanje standardne devijacije i njenog upoređivanja sa aritmetičkom sredinom, dakle, mera koja je u statistici poznata pod nazivom koeficijent varijacije. Koeficijent varijacije ili relativna standardna devijacija nije ništa drugo do pokazatelј rizika sa kojim se kalkuliše u poslovima kupoprodaje akcija. Primer za to uzima se iz berzanskog izveštaja o prodaji akcija u prethodnom periodu, koji može izgledati:
Tabela br. 1. Primer berzanskog izveštaja o cenama akcija preduzeća u istoj godini
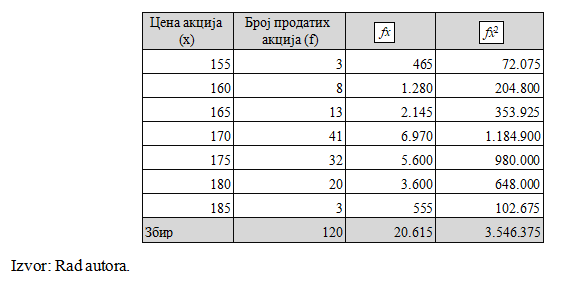

Odnosno u procentima
V = 3,71574%
Koliko iznosi koeficijent rizika od ulaganja u ovo preduzeće koji se izražava relacijom
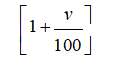
Dakle, 1,031574
Ako isto ovo preduzeće u narednoj godini proda jednak broj akcija, ali sa većim oscilacijama u prodajnoj ceni, onda će dobijeni rezultati biti bitno drugačiji.
Tabela br. 2. Primer berzanskog izveštaja o cenama akcija preduzeća u drugoj godini

Ili u procentima 7,35493%
Cena akcija u prvoj godini će biti:
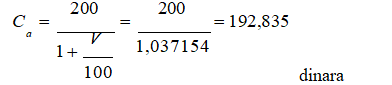
Odnosno manje od te vrednosti.
U drugoj godini cene akcija su opale i iznose
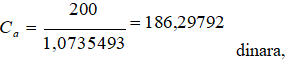
Odnosno manje od te vrednosti.
Treba imati u vidu da je to rizik za godinu dana i da se on u toku godine smanjuje po dinamici iz sledećeg obrasca:

Ako se akcija iz prethodnog primera prodaje 189-og dana u godini vrednost mase rizika na ostalim jednakim okolnostima će biti sledeća:
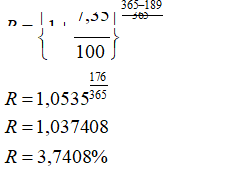
Pri tome, cena ove akcije tog dana će biti:
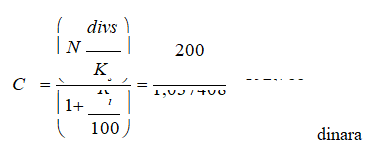
Rezonujući na ovaj način još uvek se nalazimo na rubu indiferentne pozicije. Kupac akcija na ovaj način nije ostvario nikakav dopunski efekat od kupovine akcija u odnosu na plasiranje ovih sredstava u banci. On je samo ukalkulisao rizik od ovog ulaganja, što znači da se on nalazi u položaju da mu je sve jedno hoće li kupiti akcije određenog preduzeća ili će pak svoj slobodni finansijski kapital da uloži u banku. Nјegov interes će biti zastuplјen ako ovu akciju kupi po ceni nižoj od one koja je utvđena u prethodnom obrascu. To znači da ako on nabavku akcije koja ima vrednost 186 dinara izvrši po ceni od 150 dinara, da će ostvariti dividendu veću od prinosa koji bi dobio od bankarske štednje.

Izneta argumentacija ipak nije dovolјna da se obuhvate sve relevantne činjenice u vezi sa utvrđivanjem tržišne vrednosti akcija. Na ovom sistemu dokazivanja obrazac za formiranje tržišnih cena običnih akcija glasi:
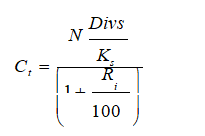
Prednji obrazac važi ako se obračun vrši u opštem slučaju. Međutim, ako se obračun vrši na određeni dan u godini zbog redukcije rizika on ima sledeći oblik:
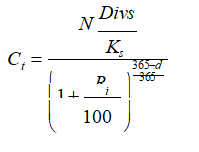
Uključivanje inflacijskih uticaja u parameter ya obrazovanje cene akcija
U slučaju da je moneta zemlјe u kojoj se vrši utvrđivanje cene akcija nestabilna plaćena cena akcija podleže revalorizaciji koja se utvrđuje za svaki dan u toku godine. Pri tom se koriste sledeće matematičke relacije.(Kočović, 2009)





Dividendu po stopi 16% računatu na nominalnu vrednost od 1.000 dinara, što donosi 160 dinara, a imajući u vidu da je on ovu akciju stvarno platio 2.517,88 dinara. To znaći da bi on na ime kamate dobio 176,25 dinara (2.517,88*9%). Formalno gledano ovaj posao nije interesantan. Stvar je međutim u tome što preduzeće čija je profitna stopa skoro dvostruko veća od proseka grane ima realne šanse da do kraja godine podigne cenu svojih akcija. To znači da će se one prodavati skuplјe. Kupovinom akcija na početku godine on plaća i očekivano poskuplјenje akcija ovog preduzeća. U ovom primeru ispostavlјa se da je ta cena 16,25 dinara (176,25-160). To znači da je kroz cenu akcija obuhvaćeno i njihovo poskuplјenje za 1,80667%. Dogodi li se da ove akcije poskupe za više, to znači da je dividendna stopa porasla te je akcionar prisvojio ekstraprihod iz dividende i poskuplјenje akcija.
Ako se anilizira kontra slučaj koji se zasniva na profitnoj stopi ovog preduzeća od 9% svi proračuni su drugačiji. Cena akcija je sledeća:
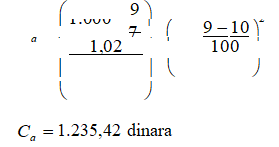
Plasiranjem ovih sredstava kod banke dobio bi se iznos od 86,48 dinara kamate (1.037,14*7%). U ovom primeru on još uvek donosi prinos od 100 dinara. Preostala razlika je cena rizika zbog posedovanja akcija preduzeća koje silazi sa scene. Sve ove pretpostavke bazirane su na stavu da se akcije kapitališu na godinu dana i u idealno stabilnim monetarnim uslovima.
2.1. Uklјučivanje inflacijskih efekata u cenu akcija koje se emituju u različito vreme
Ako se akcije emituju u različito vreme u njihovu tržišnu vrednost se inkorporira još i inflacija koja je nastala od momenta emisije do dana njihovog kapitalisanja putem naplate dividende. Ako je godišnja stopa inflacije u primeru koji je korišćen 84%, to znači da će se cena akcije koje se prodaju trećeg januara utvrditi na osnovu sledećih elemenata:


U tome je:

Do ovih podataka dolazi se na osnovu sledećih obrazaca:
A) nominalna vrednost

Nominalna vrednost se dobija iz odnosa dividende prema kamatnoj stopi. Ako je Divs 18%, a kamatna stopa 9%, to je ovaj odnos 2:1. Iz njega proizilazi da je nominalana vrednost akcije 1.850:2=925 dinara:
B) emisioni ažio
Ca - Na = Еа
Еа = emisioni ažio
1.850-925= 925
Еа =925 dinara
C) inflacijski efekat

D) Dividenda sadržana u prosečnoj vrednosti akcije
U primeru to su sledeće veličine
Div=dividenda sadržana u vrednosti akcije
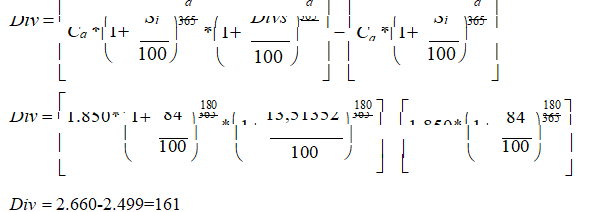
Posebna napomena: dividenda je računata na obračunsku cenu a ne na nominalnu kako se inače čini u realnom životu. Ukoliko bi se dividenda računala na nominalnu vrednost akcija onda bi se primenila stopa od
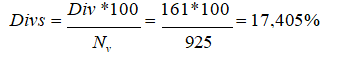
Primenom ove stope na nominalu opet bi se dobila ista vrednost dividende.
Zaključak
Odrediti pravu vrednost akcija je osnovno pitanje vezano za analizu vrednosti akcija. Ta realna vrednost je posebno značajna za investitore u akcije, finansijske analitičare, portfolio menadžere, finansijske menadžere u preduzećima i sve druge zainteresovane stejkholdere, pošto na osnovu njenog saznanja mogu zasnivati donošenje svojih investicionih odluka. Teko će investitor koji zna da je realna vrednost akcije niža od njene tekuće tržišne cene doneti odluku da ih kup i obrnuto, ukoliko je cena veća od realne najverovatnije će doneti odluku da ih proda.
Savremene teorije određivanja cene akcija zasnivaju se na tome da je cena akcija jednaka zbiru diskontovanih budućih dividendi po akciji, koje se diskontuju kamatnim stopama. Imajući u vidu da dividende direktno zavise od visine ostvarenih profita dividendne teorije se zasnivaju na predviđene buduće profite iz kojih se one plaćaju. To uslovljava da cenu akcija u budućnosti presudno određuju dva veoma značajna faktora i to budući profit i kretanje kamatnih stopa, jer kada profit raste tada i procena cene akcije raste, jer će svaki diskontovani godišnji profit rasti. Međutim ukoliko, kamatne stope rastu, vrednost akcije će biti manja jer će diskontni faktor biti veći i budući profit će se manifestovati u nižoj vrednosti akcije i obrnuto. Kamatne stope utiču i indirektno na vrednost akcija jer povećavaju troškove preduzeća, što smanjuje njihov profit, naravno u zavisnosti od strukture njihovih obaveza i načina finansiranja.
References
2.Vugdelija D,. Sedlak O. 2010. Finansijska i aktuarska matematika - osnovni koncept za nastavu; ekonomski fakultet Subotica
3.Vunjak N. 2001. Finansijski menadžment, Ekonomski fakultet Subotica
4.Đukić Đ. 1999. Utvrđivanje cena hartija od vrednosti Centar za izdavačku delatnost Ekonomskog fakulteta u Beogradu
5.Kočović J. 2009. Finansijska matematika, Centar za izdavačku delatnost Ekonomskog fakulteta u Beogradu
6.Kulić M. 2010. Finansijski menadžment, Megatrend univerzitet, Beograd
7.Rašeta J. 2008. Finansijska i aktuarska matematika, Univerzitet Singidunum, Beograd
8.Salvatore D. 1989. Theory and Problems of Managerial Economics, Mc Graw Hill Book Company, New York
9.Todorović O. 2003. Finansijska matematika, Ekonomski fakultet Niš
10.Šekarić M., Barjaktarović L. 2012. Finansijska matematika i aktuarstvo sa zbirkom zadataka, Univerzitet Singidunum, Beograd
11.Market Beaters, Valuation Methodology, www.marketbeaters.com (10.08.2016.)
12.What You Need to Know About Stocks, www.stocks.about.com (03.08.2016.)
13.www.apr.gov.rs (30.03.2016.)
14.www.belex.rs (26.09.2016.)
15.www.bloomberg.com (10.12.2015.)
16.www.investopedia.com (14.08.2016.)
17.www.investorwords.com (11.08.2016.)
18.www.finance.yahoo.com (10.09.2015.)
19.www.morningstar.com (20.08.2016.)
20.www.nyse.com (01.07.2015.)
21.www.standardandpoors.com (06.07.2016.)
22.www.stockchart.com (21.02.2016.)
23.www.valueline.com (25.08.2016.)
Published in
Vol. 4 No. 2 (2018)
Keywords
🛡️ Licence and usage rights
This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0).
Authors retain copyright over their work.
Use, distribution, and adaptation of the work, including commercial use, is permitted with clear attribution to the original author and source.
Interested in Similar Research?
Browse All Articles and Journals